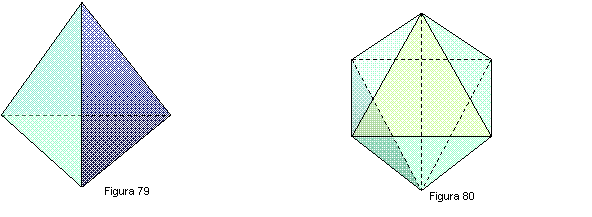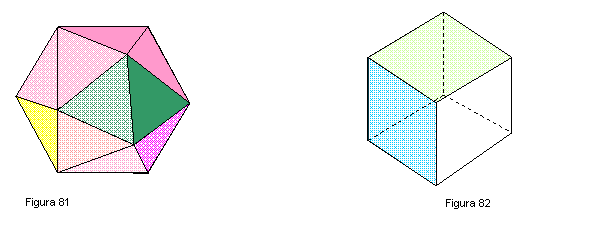| Punto | Recta | Plano | Intersección | Abatimientos y Cambios de Plano | Giros |
| Pirámide | Cono | Cilindro | Prisma | Poliedros |
OCTAEDRO: Compuesto por ocho triángulos equiláteros y seis vértices. Figura 80.
ICOSAEDRO. Poliedro compuesto por veinte triángulos equiláteros. Y doce vértices.
Figura 81.
HEXAEDRO O CUBO: Sus caras son cuadradas. Tiene seis y ocho vértices. Figura 82.
DODECAEDRO: En cada vértice concurren tres caras que son pentagonales. Tiene veinte vértices. Figura 83.
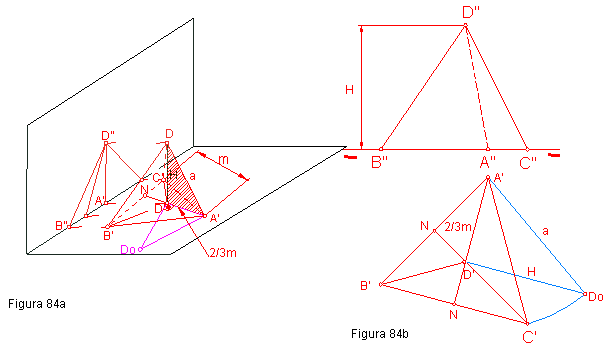
1.1. Tetraedro regular con una cara apoyada en el plano horizontal. figura 84a y b.
Tetraedro regular es el polígono regular convexo formado por cuatro caras que son triángulos equiláteros, tiene seis aristas y cuatro vértices.
La proyección horizontal será un triángulo equilátero, punto A’, B’, C’. El lado del mismo será la arista del tetraedro. El vértice del mismo se encuentra en el centro geométrico del triángulo.
Para su resolución debemos calcular el valor de la altura H de mismo. Como puede apreciarse en la figura 84 a, esta será igual al lado de un triángulo rectángulo, cuyo cateto es 2/3 de la mediana del triángulo, y tiene como hipotenusa la arista del tetraedro a.
Una vez hallad ala altura H, bastará con traza runa perpendicular a la línea de tierra que pase por D’ y llevar sobre ella el valor hallado, ya que estas e encuentra en verdadera magnitud por ser perpendicular al plano horizontal.
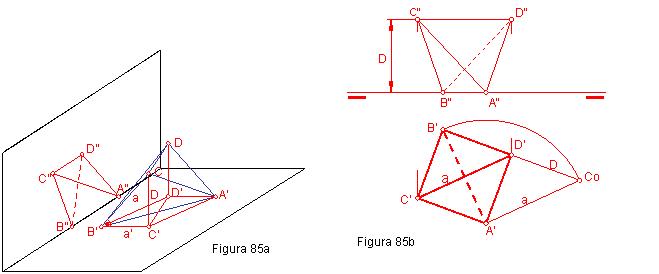
1.2. Tetraedro regular con dos aristas opuestas paralelas al plano horizontal. figura 85 a y b.
Las aristas A-B y C-D, se proyectan en el plano horizontal en verdadera magnitud formando un cuadrado cuyos lados son las proyecciones de las arista sen el horizontal y sus diagonales las arista sen verdadera magnitud.
La distancia D entre las aristas que CD y C’D’, figura 85 a, vendrá dada por el lado D de un triángulo rectángulo, de cateto la proyección del a arista a’ y de hipotenusa el valor de la arista a. Figura 85 b.
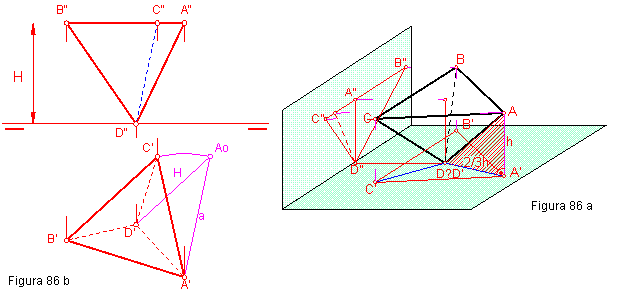
1.3. Tetraedro regular con un vértice apoyado en plano horizontal. Figura 86 a y b.
La proyección horizontal del tetraedro apoyado con un vértice D en el plano horizontal, será un triángulo equilátero, cuyo lado será igual a la arista del mismo.
El ejercicio quedará resuelto cuando conozcamos la altura del mismo. Dicha altura se calculará de forma similar a la del tetraedro apoyado con una cara en el plano horizontal.
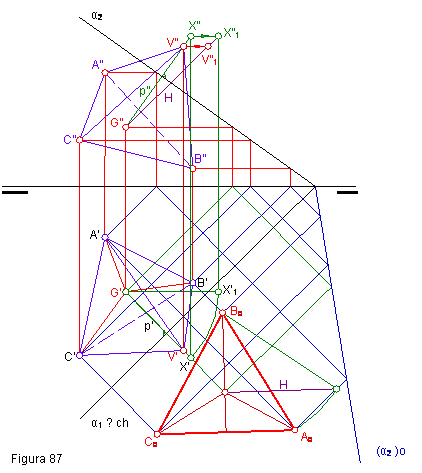
1.4. Dada la proyección horizontal de un tetraedro, dibujarlo teniendo en cuenta que se encuentra apoyado en el plano oblicuo α. Figura 87
- Hallaremos la verdadera magnitud de la base. Para ello abatimos el triángulo A’, B’, C’, utilizando como charnela la traza vertical del plano, α2.
- Un vez que tenemos el triángulo equilátero correspondiente a las caras del tetraedro, hallamos la altura del mismo. Procedimiento visto anteriormente.
- Seguidamente hallamos las proyecciones, horizontal y vertical del ortocentro G.
- El siguiente paso, consistirá en hallar la proyección vertical del triángulo A’, B’, C’.
- Como el tetraedro se encuentra apoyado en el plano α , la altura del mismo será una recta perpendicular a la traza del plano. Una vez trazada la altura, elegimos un punto cualquiera X’ de la recta p’.
- Obtenemos la verdadera magnitud del segmento G’- X’, realizando un giro de la misma. Punto X”1-X’1
- Sobre la recta G”– X”1, llevamos la altura H del tetraedro, que por medio de una paralela a la línea de tierra, obtenemos V” y V’
- la unión del vértice con los puntos A, B, y C, nos determinan el tetraedro.
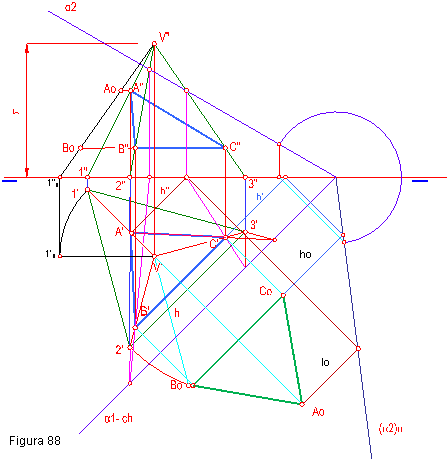
1.4.1. Representar el tetraedro regular de base 1’, 2’, 3’, apoyado en el plano horizontal. Seguidamente determinar :
- Sus proyecciones y verdadera magnitud de la sección interceptada por el plano oblicuo α.
- Hallar el desarrollo del mismo. Figura 88.
- Hallar el vértice V, y las aristas de las caras.
- Hallar la altura del tetraedro. Lado de un triángulo rectángulo de hipotenusa la arista y lado menor 2/3 de la mediana
- Para hallar la proyección horizontal de la sección Utilizaremos el procedimiento de intersección de aristas y homotecia.
- Por los puntos A’, B’, C’ se levantan perpendiculares a la línea de tierra hasta que corte a las aristas en los puntos A”, B”, C”.
- Para hallar la verdadera magnitud abatimos el plano vertical.
- Seguidamente abatimos las horizontales de plano h’ y l’ que nos determinan ho y lo.
- Para hallar la verdadera magnitud de la sección tendremos que girar una de las aristas del tetraedro, por ejemplo la V’ 1’. La verdadera magnitud de la arista vendrá dada por el segmento 1”1 V”. Tazando paralelas a la línea de tierra por los punto A” y B” tendremos Ao, Bo y Co.
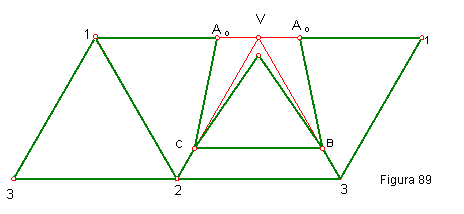
- Para dibujar el desarrollo, trazaremos las caras laterales del tetraedro, que son cuatro triángulos equiláteros. Figura 89.
1.5. HEXAEDRO O CUBO.
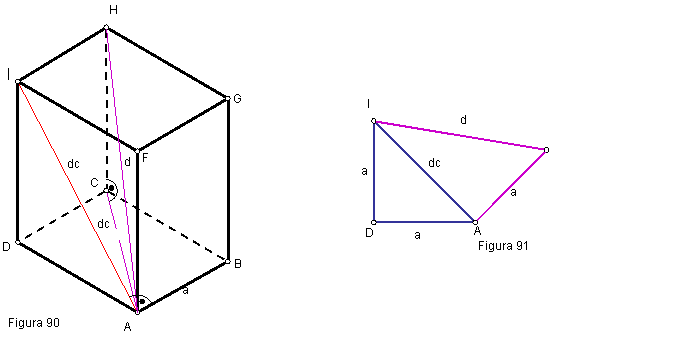
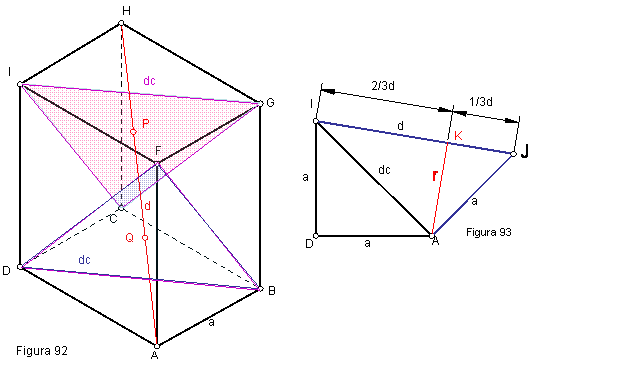
Poliedro formado por seis caras que son cuadrados, tiene doce aristas y ocho vértices, sus ángulos son rectos formando un triedro trirrectángulo. Los elementos que lo definen son: La arista a, la diagonal de la cara dc y la diagonal del cubo d.
Como puede observarse, Figura 90, la diagonal de la cara es la hipotenusa de un triángulo rectángulo cuyos lados son las aristas del mismo.
La diagonal del cubo dc es hipotenusa de un triángulo rectángulo que tiene como catetos la diagonal de la cara dc y la arista a. Figura 91.
Si dividimos la diagonal del cubo en tres partes iguales, puntos P, Q, (figura 92), y trazamos planos perpendiculares a dicha diagonal que pasen por los referidos puntos, estos interceptarán a las caras formando triángulos equiláteros iguales BDF y CGI.
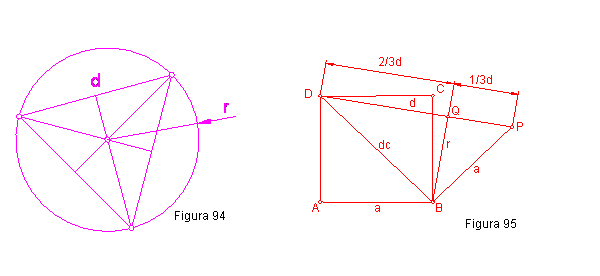
La altura r (Figura 94), del triángulo AJI, es el radio de la circunferencia circunscrita al triángulo equilátero de lado la diagonal de la cara, dc. El pie de esta perpendicular K divide a la hipotenusa IJ en 2/3d y 1/3 d. propiedad que utilizaremos para resolver el problema que veremos a continuación.
1.5.1. Hexaedro con una diagonal perpendicular al horizontal. Figura 96.
De acuerdo con lo expuesto anteriormente tendremos que hallar el radio r de la circunferencia circunscrita al triángulo equilátero de lado la diagonal de la cara dc. Figura 95.
Haciendo centro en A’, punto cualquiera, de la diagonal, se trazan los triángulos B’, E’, D’ y C’, F’,H’, obteniendo la proyección horizontal.
Llevamos a una recta perpendicular a la línea de tierra por A’ el valor de la diagonal hallada d y la dividimos en tres partes, haciendo pasar por las divisiones dos planos δ2 -φ2 paralelos al horizontal.
Seguidamente proyectamos los vértices del cubo en proyección horizontal hasta que se corten con las trazas de los planos δ2 y φ2 obteniendo sus proyecciones verticales.
Se puede observar que el radio r puede hallarse abatiendo el triángulo rectángulo A”, C”,G”.
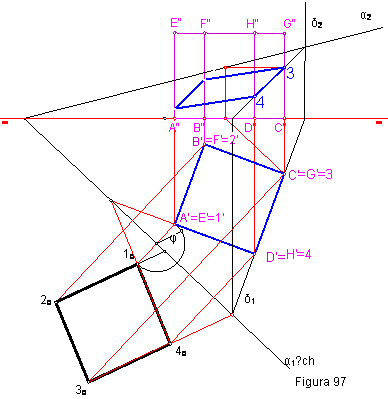
1.5.2. En la figura dada se define un hexaedro mediante su proyección horizontal. Sabiendo que dicho poliedro se encuentra apoyado en el plano de proyección horizontal, determinar:
- Su proyección vertical.
- Obtener posteriormente en proyección y verdadera magnitud la sección producida por el plano α. Figura 97.
Como puede observarse la proyección horizontal de la sección 1’, 2’, 3’ 4’, se confunde con la base del cubo. La proyección vertical se obtendrá por medio de rectas horizontales o frontales, punto 3’-3”. También se puede resolver haciendo contener a las aristas en un plano auxiliar.
Para obtener la verdadera magnitud operaremos abatiendo el vértice 1 por el procedimiento general, y operando para los restantes puntos por afinidad.