Alfabeto de la Recta

Punto

Recta

Plano

Intersección

Abatimientos y Cambios de Plano

Giros

Pirámide

Cono

Cilindro

Prisma

Poliedros

1. 1. LA RECTA

Una recta queda definida por dos puntos. Por tanto para su representación bastará con determinar sus proyecciones, y unir las correspondientes proyecciones homónimas de sus puntos.

Un punto pertenece a una recta si sus proyecciones homónimas se corresponden con la recta.

1.1. NOMENCLATURA DE LA RECTA.

Para su denominación utilizaremos letras minúsculas acompañadas de una o dos comillas, según sea la proyección horizontal o vertical. (Por ejemplo r’, r”). Los puntos que definen las rectas se designaran por letras mayúsculas.

Una recta queda definida por sus trazas. Existen dos trazas una horizontal y otra vertical.

Se denomina traza al punto de intersección de la recta con los planos de proyección.

Traza horizontal se representa por H, su proyección será por tanto H’ acompañada de la letra minúscula correspondiente a la recta.  Por ejemplo H’r.

Traza vertical se representa por V, su proyección vertical será por tanto V” acompañada de la letra minúscula correspondiente a la recta. Por ejemplo V”r.

Como H y V siempre serán coincidentes con sus respectivas proyecciones H’ y V”, en lo sucesivo solo emplearemos su proyecciones.

1.2. PROYECCIÓN DE UNA RECTA OBLICUA DADA POR DOS PUNTOS DE ELLA.

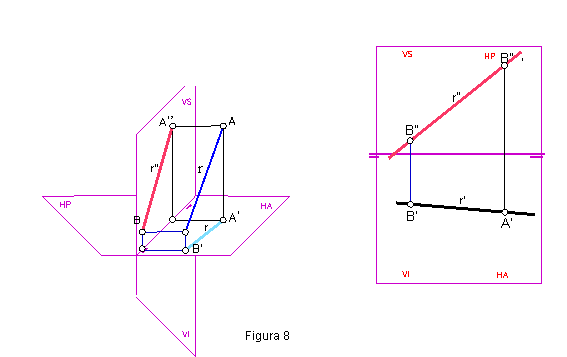
Se la recta r, dada por los puntos A y B. Figura 8.

Hallamos las proyecciones horizontal de los puntos A’ y B’. Seguidamente hallamos la vertical, A” y B”. la unión de ambas nos determinará las proyecciones r’ y r” del a recta r.

1.3. PROYECCIÓN DE UNA RECTA OBLICUA MEDIANTE SUS TRAZAS.

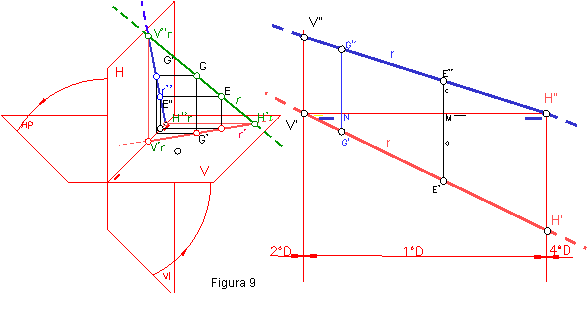
Sea la recta  r que corta a los planos de proyección en los puntos H ≡ H’r y V≡ V”r, trazas de la misma. Al ser las trazas de la  recta puntos de la misma, bastará con unir sus proyecciones homónimas para obtener las proyecciones r’-r”. El resultado será el mismo que si hubiéramos proyectado los puntos G y E, pertenecientes a la recta. Figura 9.

1.4. RECTA PARALELA AL PLANO VERTICAL, PRIMER CUADRANTE RECTA FRONTAL.

Tendrá una sola traza la horizontal H ≡ H’, y su proyección horizontal será paralela a la línea de tierra. La vertical formará un determinado ángulo con el plano horizontal. Figura 10.

Para hallar los puntos de intersección de la recta con los bisectores, bastará con buscar en la recta un punto cuya cota sea igual al alejamiento si se encuentra en el primer o tercer bisector, o bien que ambas sean coincidentes si se encuentran en el segundo y cuarto.

La recta será visible si se encuentra en el primer bisector, en caso contrario será oculta y se representará por líneas de trazos.

Los referidos puntos se representarán por x o y primero y segundo bisector respectivamente.

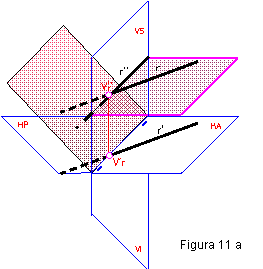
1.5. PROYECCIÓN DE UNA RECTA PARALELA AL PLANO HORIZONTAL O RECTA HORIZONTAL.

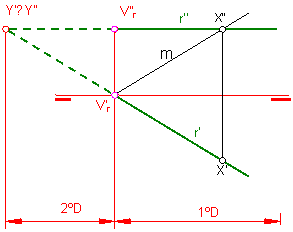
Estará contenida en un plano paralelo al horizontal. Cortará únicamente al plano vertical. Tendrá la traza vertical paralela a la línea de tierra. El punto de corte de la recta con el segundo bisector tendrá la misma cota que alejamiento. Figura 11 a y b.

Para hallar el punto de corte con el primer bisector trazaremos una recta auxiliar m, que formará el mismo ángulo con la línea de tierra que r’. El punto X’-X” será el punto de corte con el primer bisector. Figura 11 b.

1.6. RECTA PARALELA AL PLANO VERTICAL SEGUNDO CUADRANTE.

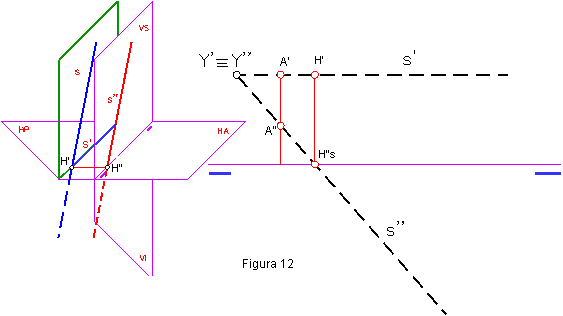
Será igual que la anterior, pero no será visible. El punto de intersección con el bisector estará por encima de la línea de tierra. Figura 12.

1.7. RECTA PERPENDICULAR AL PLANO VERTICAL. RECTA DE PUNTA (s).

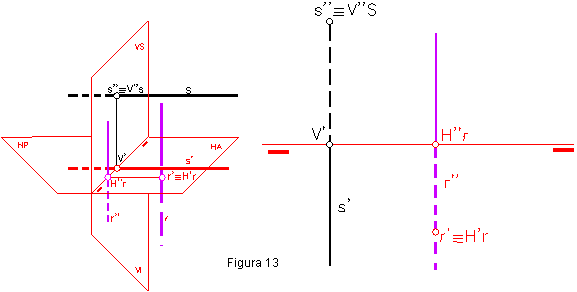
La proyección vertical será un punto, s” que será coincidente con la traza vertical V”s. La horizontal será una recta perpendicular  a la línea de tierra.Figura 13.

1.8. RECTA PERPENDICULAR AL PLANO HORIZONTAL, RECTA VERTICAL (r).

Será contraria a la anterior.

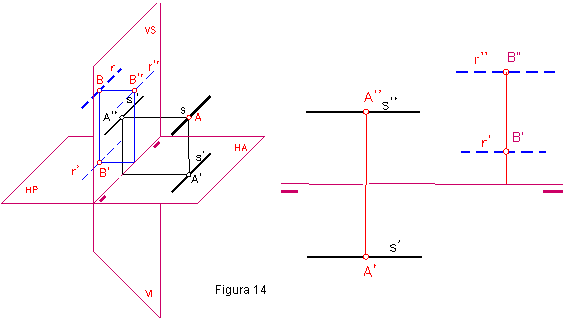
1.9. RECTAS PARALELAS A LA LÍNEA DE TIERRA. (figura 14)

No cortará los planos de proyección y por tanto no tendrá trazas.

Para su representación tendremos que dibujar un punto cualquiera de la recta. Punto A de la recta s y B de la recta r.

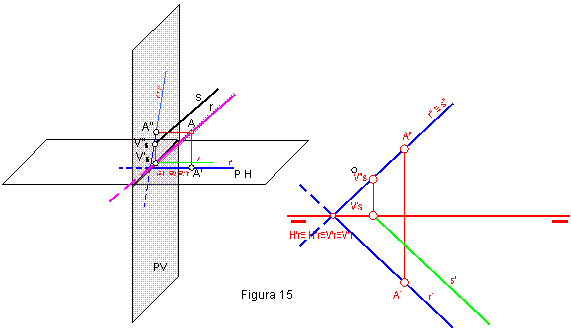
1.10. RECTA – r – CONTENIDA EN EL PRIMER BISECTOR.

Todas sus trazas estarán en la línea de tierra y formará 45º con los planos de proyección. Figura 15.

1.11. RECTA – s – PARALELA AL PRIMER BISECTOR.

Estará contenida en un plano paralelo al bisector, su traza horizontal será paralela al bisector. Figura 15.

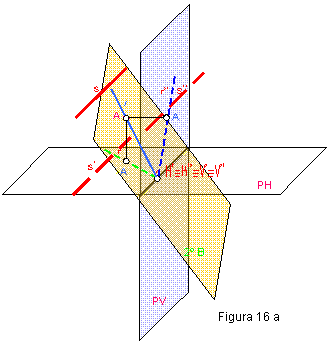
1.12. RECTAS CONTENIDAS EN EL SEGUNDO BISECTOR.

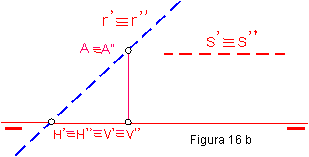
Formará 45º con los planos de proyección, r’- r” serán coincidentes. Ambas serán ocultas. Figura 16 a y b.

1.13. RECTA – s – PARALELA A LA LÍNEA DE TIERRA.

Sus proyecciones serán coincidentes. No tiene ninguna traza. Será preciso fijar un punto cualquiera de la recta. Figura 16 a y b.

1.14. RECTA PERPENDICULAR A LA LÍNEA DE TIERRA, CORTÁNDOSE CON ELLA.

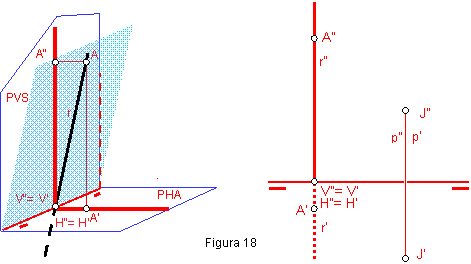
Es un caso particular de las rectas de perfil, todas las trazas se encontrarán en la línea de tierra. Para que quede definida será preciso situar un punto cualquiera de ella. Punto A. Figura 18.

Estas rectas estarán contenidas en un plano perpendicular a la línea de tierra. Sus proyecciones son coincidentes en un mismo punto de la línea de tierra.

Si la recta estuviera contenida en un plano bisector, recta p (p’-p”), sus proyecciones serian las mismas, con la salvedad que cualquier punto de la recta p.e J, tendría la misma cota que alejamiento.

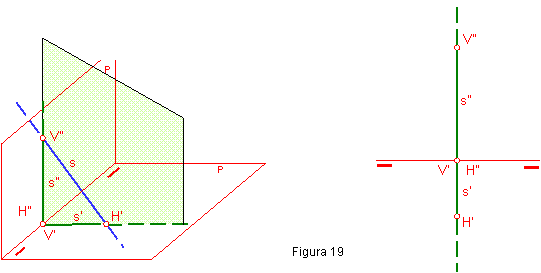
1.15. RECTA PERPENDICULAR A LA LÍNEA DE TIERRA, CRUZÁNDOSE CON ELLA. RECTAS DE PERFIL.

La recta s, estará contenida en un plano  α, perpendicular  a los planos de proyección. Sus trazas estarán en una línea perpendicular a  la línea de tierra y sus proyecciones V’- H”, serán coincidentes. Figura 19.

1.15.1. TERCERA PROYECCIÓN DE UNA RECTA DE PERFIL.

Para definir una recta de perfil será preciso representar la tercera proyección de la misma. Figura 20.

Tazamos un plano de perfil PP. Giramos la traza horizontal H’_r, hasta que ocupe la posición (H’_r),  que uniéndola con V”_r, tendremos la tercera proyección de la recta r”’.

1.16. HALLAR LA TERCERA PROYECCIÓN DE UNA RECTA QUE PASA POR LA LÍNEA DE TIERRA.

Sea la recta r ( r’, r”) dada por los puntos A (A”, A’) y B (B’, B”)

Sus trazas y proyecciones están  confundidas en una misma recta perpendicular a la línea de tierra. Figura 21.

1. Elegimos un plano cualquiera  de perfil π.

1. Llevamos  la recta a tercera proyección, obteniendo la recta r”.

Figura 21

Ir al Principio