| Punto | Recta | Plano | Intersección | Abatimientos y Cambios de Plano | Giros |
| Pirámide | Cono | Cilindro | Prisma | Poliedros |
Decimos que abatimos un plano sobre otro, cuando hacemos superponer el primeros sobre el segundo, haciendo girar alrededor de un eje, llamado charnela, que es la intersección de ambos. Con los abatimientos se pretende obtener verdaderas magnitudes de rectas o figuras planas.
1.- Para abatir un punto P, situado en el plano α , abatimos dicho plano α que contiene al punto P, utilizando como charnela la intersección de los planos α y δ. Línea a-b. Figura 62 a.
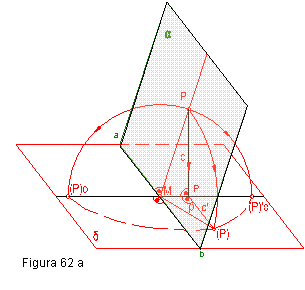
2.- El radio de giro será la mínima distancia del punto a la charnela, la cual se halla como hipotenusa del triángulo rectángulo cuyos catetos
son P’ M y P’ (P).
Una vez visto el proceso en el espacio, trabajaremos en el plano.
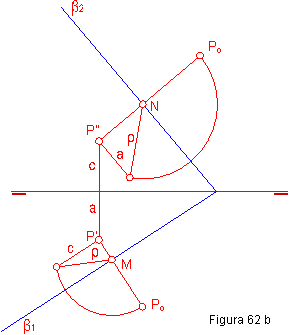
Sea el punto P ( P’-P”).
1.- El primer paso será hallar el radio de giro ρ. Por P’, trazamos una perpendicular y una paralela a la traza horizontal α1, que la utilizamos como charnela.
2. Sobre la paralela, llevamos el valor de la cota del punto c.
3.- Haciendo centro en M y con radio ρ, trazamos un arco hasta que corte a la perpendicular P’ en Po, punto abatido.
Hemos realizado el abatimiento en el plano horizontal, podemos repetir la caso, el alejamiento en lugar de la cota. Figura 62 b.
1.1. ABATIMIENTO DE PUNTO, RECTA Y TRAZA DEL PLANO.
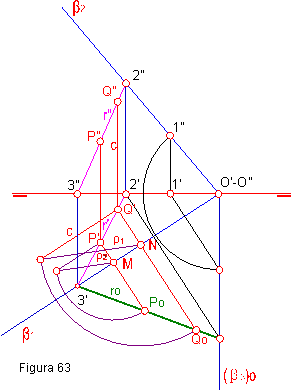
1.- Sea una recta r(r’-r”). Figura 63.
2-. Elegimos dos puntos cualquiera de la recta, por ejemplo, los puntos P y Q y los abatimos, caso anterior.
3.- La unión de Po y Qo, puntos abatidos será la recta ro, abatida.
4.- Para abatir las traza del plano, basta con abatir dos puntos de la misma. El punto O’-O” se encuentra abatido por ser punto doble, por tanto abatiremos únicamente el punto 1’-1”.
5.- La verdadera magnitud de la recta también puede obtenerse abatiendo las trazas de la misma. 2’-2”. La traza 3’ por encontrarse en la charnela queda batida en si mismo.
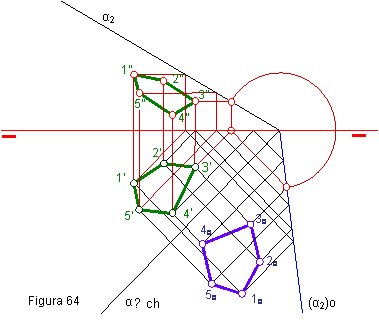
1.2. ABATIMIENTO DE UNA FIGURA CUALQUIERA .(figura 64)
1.- Partimos de un pentágono irregular, de vértices 1’, 2’, 3’, 4’, 5’, apoyado en el plano horizontal.
2.- Hallamos la proyección vertical, 1”, 2”, 3”, 4”, 5”. del pentágono, aunque esta no es necesaria para obtener la verdadera magnitud. Lo hacemos por medio de
horizontales de plano.
3.- Para hallar la verdadera magnitud de la figura, utilizaremos como charnela la traza α1. Abatimos el la traza vertical α2 del plano.
4.- Seguidamente abatimos las rectas horizontales de plano que pasan por los vértices del pentágono.
4.- Seguidamente abatimos las rectas horizontales de plano que pasan por los vértices del pentágono.
4.- Seguidamente abatimos las rectas horizontales de plano que pasan por los vértices del pentágono.
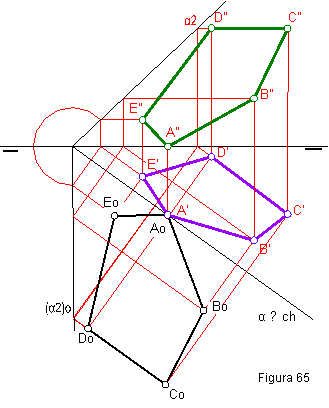
1.3. DADA UNA FORMA POLIGONAL Ao, Bo, Co, Do, DETERMINAR SU PROYECCIÓN HORIZONTAL Y VERTICAL, UTILIZANDO COMO CHARNELA LA TRAZA HORIZONTAL DEL PLANO. (figura 65)
1. Hallaremos la traza vertical del plano α.
2.- El punto A por encontrarse en la charnela es un punto doble, por lo tanto Ao ≡A’.
3. Mediante horizontales de plano hallaremos el resto de los puntos.
2. CAMBIOS DE PLANO
Los cambios de plano tienen como objetivo permaneciendo fija la posición de la figura en el espacio variar uno de los planos de proyección de forma que este se coloque en una posición adecuada que nos facilite la representación del objeto.
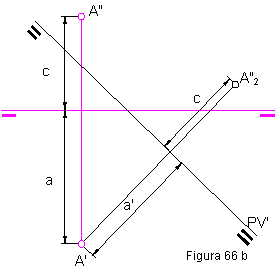
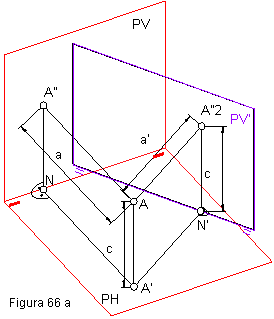
Cuando varían los planos, cambia la posición de la línea de tierra. Esta nueva línea de tierra se representa por dos trazos gruesos. Figura 66 a y b.
El punto A”2 cambia de posición conservando el valor de la cota c. El punto A’ permanece fijo, variando el valor del alejamiento a. Figura 47 a y b.
2.1. CAMBIO DE UNA RECTA OBLICUA A PARALELA AL HORIZONTAL.( HORIZONTAL DE PLANO)
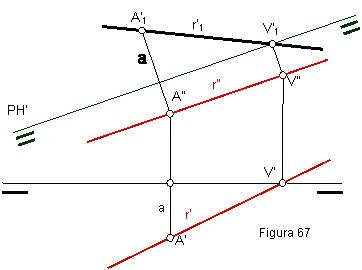
Elegimos una nueva línea de tierra paralela a la traza vertical del plano ya que la proyección vertical de la recta será paralela a la L.T. Para ello cambiamos el plano horizontal.
Cambiamos dos de los puntos de la recta, por ejemplo una de sus trazas V y un punto cualquiera A. Figura 67.
2.2. CAMBIO DE LAS TRAZAS DE UN PLANO OBLICUO CUALQUIERA.
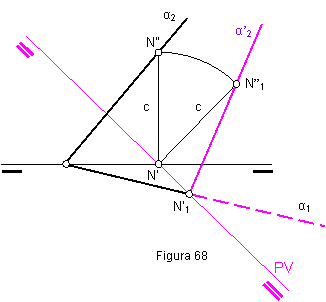
1.- Elegimos una nueva línea de tierra.
2.- Trazamos por el punto N’, cruce de las dos líneas de tierra, las rectas perpendiculares a cada una de ellas.
3.- Llevamos sobre la perpendicular a la nueva línea de tierra el valor de la cota c de punto N. Figura 68.
2.3. CAMBIO DE LAS TRAZAS DE UN PLANO OBLICUO A PLANO PROYECTANTE VERTICAL.
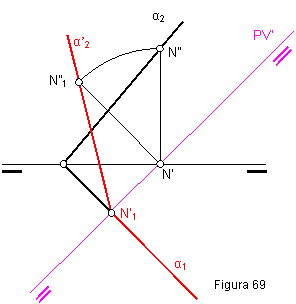
Elegiremos la nueva línea de tierra perpendicular a la traza horizontal α1. Figura 69.
El resto del ejercicio es similar al anterior.
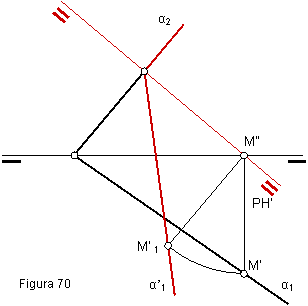
2.4. CAMBIO DE LAS TRAZAS DE UN PLANO OBLICUO A PLANO PROYECTANTE HORIZONTAL.
En este caso la nueva línea de tierra será perpendicular a la traza vertical. Figura 70.