- REPRESENTACIÓN DE FIGURAS PLANAS EN EL SISTEMA ISOMÉTRICO.
3.1.1 Representación de la Circuferencia
La circunferencia situada en una de las caras, se proyecta sobre el cuadro como una elipse. En este sistema la única dificultad que podemos encontrar es, precisamente, la representación de la circunferencia.
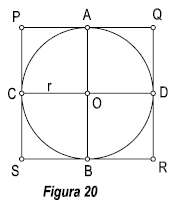
Vamos a trazar la perspectiva de una circunferencia situada en los tres planos del sistema. XOY, XOZ, YOZ. Inscribimos la circunferencia en un cuadrado de lado, el diámetro de la misma. Dividimos dicho cuadro en cuatro partes iguales. ( Figura 20).
Se dibuja en las tres caras del triedro, dicho cuadrado, cuyo resultado será un rombo. Las rectas AB y CD, serán los diámetros conjugados de la elipse.
Según se desprende de la figura 23, el diámetro mayor de la elipse a, b, se corresponde con el de la circunferencia, y es perpendicular al eje no contenido en la cara, y el menor paralelo al mismo.
El resto de la construcción puede derivarse del análisis de la figura 23.
El trazado de la misma se realizará por medio de puntos, plantillas especiales, o bien haciendo uso un gráfico para la construcción de elipses isométricas aproximadas de cuatro u ocho centros, procedimientos que nos contemplamos en este tratado.
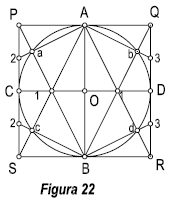
Para facilitar su construcción podemos utilizar el procedimiento que se describe a continuación, Método de los ocho puntos. (Figura 22 y 23).
Inscribimos la circunferencia en un cuadrado de lados P , Q, R, S, siendo los puntos A, B, C, D, los puntos medios de los lados del cuadrado. Hallamos los puntos 2 y 3, puntos medios de los segmentos PC y QD. Unimos dichos puntos con A y B, nos determinan los puntos a, b, c, d,. Transformamos dicho cuadrado en isométrico, rombo P, Q, R, S. Unimos A con R y S y B con Q y P. Hallamos los puntos medios de los segmentos PC y QD, que nos determinan los puntos 2 y 3. El resto de la construcción se deduce de la figura 23.
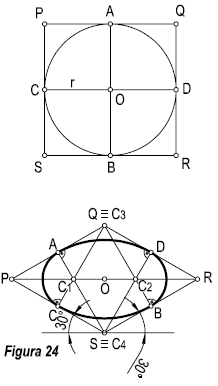
Para facilitar el trazado, podemos sustituir la elipse por un óvalo de cuatro centros. Representemos la elipse proyección de la circunferencia de centro O y radio r. Dicha circunferencia la inscribimos en un cuadrado de lados P , Q, R, S, siendo los puntos A, B, C, D, los puntos medios de los lados del cuadrado. Transformamos dicho cuadrado en isométrico, rombo P, Q, R, S, por el punto Q, trazamos dos perpendiculares a la recta SRy SP. Y por el punto S, trazamos otras dos perpendiculares a las rectas PQ y QR. Dichas perpendiculares se cortan en los puntos C1 y C2 que con los C3, y C4, nos determinan los centros de curvatura del óvalo. (Figura 24).
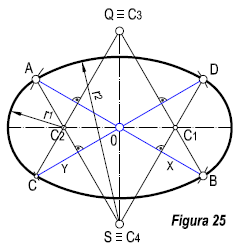
Podemos representar la curva, por el método de los diámetros conjugados. Método de cuatro centros.
Por el centro O de la elipse, trazamos dos diámetros conjugados, de 30º con la horizontal, que representan los ejes X e Y. A partir del centro, llevamos el radio de la circunferencia, reducido 0,816r, si estamos trabajando con reducción. Los puntos A, B, C, D, representan los extremos de los diámetros conjugados.. Por el punto medio de BO, trazamos una perpendicular, que corta al eje mayor en el punto C1. Repetimos la operación, para C2, C3, y C4, que nos determinan los centros de curvatura de la curva.( Figura 25).
3.1.2 Representación del Triángulo
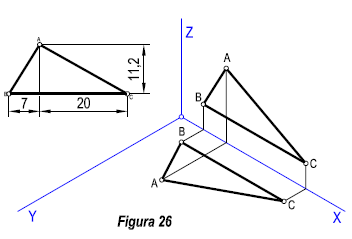
Trazamos la altura del triángulo, dividiendo la base en dos segmentos. Trazamos la base paralela a unos de los ejes, por ejemplo al eje X. la altura será paralela al eje Y, llevamos el valor de la basealtura, y los segmentos en que esta divide a la base, sobre los segmentos en axonométrico, bien reducidos o a escala natural, según convenga.
Terminamos uniendo los vértices. (Figura 26).
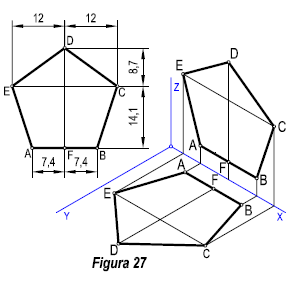
3.2.3 Representación del Pentágono
Dividimos el pentágono en cuatro partes, tal y como se indica en la figura 27. Trazamos la recta DF, paralela al eje Z, y la EC, paralela al eje X. Sobre dichas paralelas llevamos el valor de dichos segmentos, que nos determina los puntos, A, B, C, D, E.
3.2 Trazado de perspectivas Isométricas
Para el trazado de una perspectiva, podemos utilizar dos procedimientos:
a) Partiendo del cubo de envoltura de la pieza.
b) Por medio de las proyecciones previas, obtener la proyección directa.
En ambos casos debemos de partir de las proyecciones diédricas del objeto.
3.2.1. Partiendo del cubo.
Partimos de las proyecciones diédricas acotadas del objeto. ( Figura 28).
El procedimiento consiste en dibujar el prisma que envuelve la pieza e ir eliminando material de la misma hasta obtener el objeto deseado.
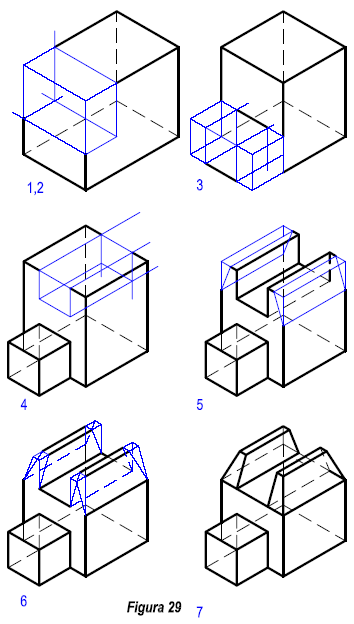
Los pasos a seguir se indican en la figura 29.
Primero: Dibujamos el cubo de la envoltura.
Segundo: Eliminamos el material que forman el escalón.
Tercero: Eliminamos el material sobrante para formar el dado.
Cuarto: Dibujamos el vacío del cuerpo.
Quinto: Dibujo de la oblicuidad. Para ello dibujamos las líneas que nos limitan la oblicuidad.
Sexto: Dibujamos las líneas que nos limitan la segunda oblicuidad.
Séptimo: La figura queda terminada.
3.2.2. Partiendo de las proyecciones previas.
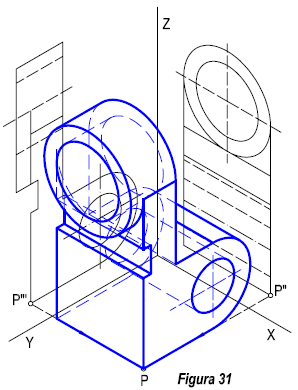
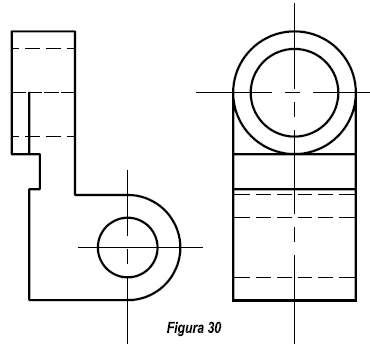
En este caso, también iniciaremos la perspectiva partiendo de sus proyecciones diédricas. ( Figura 30).
El primer paso será dibujar los ejes X, Y, Z. Para continuar dibujando las proyecciones de la pieza, sobre las caras, XOZ y YOZ. No será preciso dibujar la tercera proyección. Conociendo dos de sus proyecciones podemos obtener la tercera. Para ello trazaremos restas paralelas a los ejes X, Y, por los puntos, P” y P”’, estas rectas se cortarán en el punto P, que será un punto de la perspectiva. De la misma forma se obtienen el resto de los puntos. ( Figura 31).
Al Principio de la Página
Año 2008