- TIPOS DE PERSPECTIVAS.
En esta segunda parte, trataremos la aplicación de los conceptos expuestos anteriormente, realizando el trazado de distintos elementos.
El trazado de una perspectiva representa un cierto esfuerzo, pero este se ve recompensado, cuando se encuentra totalmente terminado y podemos observar la bondad del mismo.
Este tipo de trazados, contrarios al dibujo artístico, es totalmente objetivo, dosificado y programado, que siguiendo las indicaciones que expondremos más adelante, se puede obtener un resultado bastante satisfactorio.
Según el ángulo que forme el plano del cuadro con los ejes del sistema, la proyecciones se dividen en:
a) Proyección isométrica
b) Proyección dimétrica
c) Proyección trimétrica.
Seguidamente se estudiarán cada una de ellas.
Para comprender esta parte, se deberá tener un conocimiento amplio de los expuesto con anterioridad.
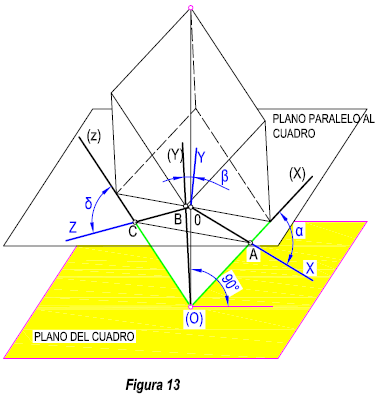
Consideremos un cubo apoyado en el plano del cuadro, de forma que la diagonal (O) M, sea perpendicular al mismo. (Figura 13). Las aristas que concurren en (O), serán los ejes del sistema X, Y, Z. Si dicho cubo lo cortamos por un plano paralelo al cuadro, su intersección con dicho plano, nos determinará el triángulo de trazas A, B, C. (figura 13).
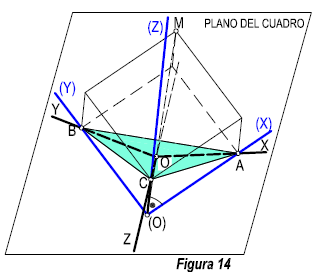
Para una mayor claridad, situaremos el cubo en la posición de la figura 14. El triángulo de trazas en verdadera posición es, equilátero, y los ángulos que forman los ejes en el espacio (X), (Y), (Z), con los proyectados en el cuadro X, Y, Z, son iguales α = β = δ. Este sistema se llama isométrico. Por tanto las escalas de reducción en los tres ejes serán iguales y como consecuencia la distorsión producida será idéntica en las tres caras del sistema.
2.1.1. Coeficiente de reducción
Si hacemos que: (O) A = (O) B = (O) C = a. (figura 14)
En el triángulo A(O)C, se verifica que:
AB = =; relación que existe entre la diagonal y los lados de un cuadrado. Dicha relación se cumple para las tres caras del cubo, luego
AB = BC = CA =
En el triángulo CBD, figura 8, se verifica que:
= = = =
siendo OC = 2/3 de CD, sustituyendo, tendremos que:
El coeficiente de reducción será la relación entre:
Valor ya calculado cuando se hablaba del Teorema de Schlömilch- Waisbasch.
Una vez que conocemos el coeficiente de reducción, la escala axonométrica se obtendrá, multiplicando el valor de la unidad real por 0,816, es decir:
e x = e y = e z = 0,816 e de esta forma queda claro la diferencia entre la escala axonométrica y el coeficiente de reducción..
Para evitar las operaciones que conlleva realizar una perspectiva y, basándonos en los conocimientos expuestos con anterioridad, construiremos una escala gráfica.
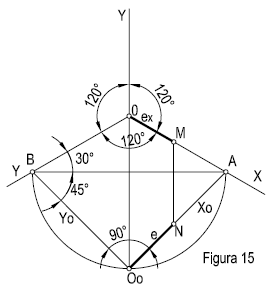
Los tres ejes se proyectan sobre el cuadro formando un ángulo de 120º entre si y con la misma reducción. (Figura 15).
Trazamos, perpendicularmente al eje Z, una recta cualquiera AB, seguidamente, abatimos el triángulo rectángulo ABO, utilizando como charnela la traza AB, para ello trazamos una circunferencia que pase por AB. El punto Oo, será el vértice del triedro abatido. Las rectas Oo A y Oo B, serán los ejes abatidos.
Sobre la recta OoA, se lleva una magnitud real e, y mediante la perpendicular a la charnela MN, se determina magnitud reducida ex.
La relación entre OA/Oo A = 0,816
Basándonos en lo anterior trazaremos una escala gráfica.
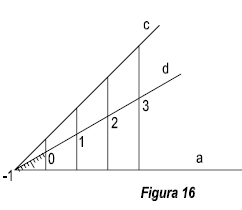
En el extremo de una recta cualquiera a, trazamos dos rectas, una a 45º, recta c, y otra a 30º recta d. Sobre la recta c, llevamos divisiones de 1 cm. Seguidamente por dichas divisiones trazamos perpendiculares a la recta a, las divisiones obtenidas en la recta d, serán de 1 cm a escala0,816. Para medir las décimas del cm. Realizamos una contra escala, dividiendo en diez partes la primera división. ( Figura 16)
2.1.2. CARACTERÍSTICAS DEL DIBUJO ISOMÉTRICO
Un dibujo isométrico no es una perspectiva isométrica, ya que se realiza si reducción alguna. Este, al igual que la perspectiva isométrica, nos revela las caras del sólido en los tres sectores de los ejes, con la misma amplitud.
Un dibujo isométrico es sensiblemente mayor que el modelo real, exactamente 1,225.
Para el dibujo isométrico clásico existen tres formas de representarlo. (Figura 17).
- Método normal ( visto por la parte superior).
- Método de ejes invertidos ( visto desde la parte inferior)
- Con el eje principal horizontal.
Este sistema se analizará de forma muy elemental.
Tiene dos escalas métricas iguales, y el triángulo de trazas es isósceles.
La perspectiva dimétrica normalizada, está recogida en la norma UNE 1-035-75 y posteriores, y está basada en el sistema axonométrico, cuya relación de escalas, ex, ey, ez es 1 : ½ : 1, sus valores serán, cos α = cos β = 0,942; cos δ = 0,471. El ángulo ZOX = 97º, 10’; y los ángulos YOZ = XOY = 131º 25’.
Podemos observar que la reducción de los segmentos en los ejes Xy Z, es muy pequeña, menor del 6%, y la reducción de los segmentos en el eje Y, es aproximadamente la mitad.
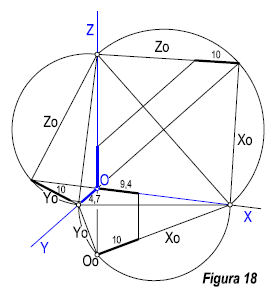
La construcción de la escala gráfica es similar al sistema isométrico, con la salvedad de que hay que dibujar las escalas para dos ejes.( Figura 18 ).
Sobre los ejes en verdadera magnitud hemos llevado 10 mm. la reducción sobre el eje X = Z = 9,4 mm. y sobre el eje Y = 4,7 mm.
Para simplificar estos valores, podemos tomar la medida real en los ejes X e Z, y la mitad en el eje Y.
Únicamente diremos que el triángulo de trazas es escaleno, y que la reducción en los tres ejes es diferente. La obtención de la escala se realiza por el mismo procedimiento que los dos casos anteriores.
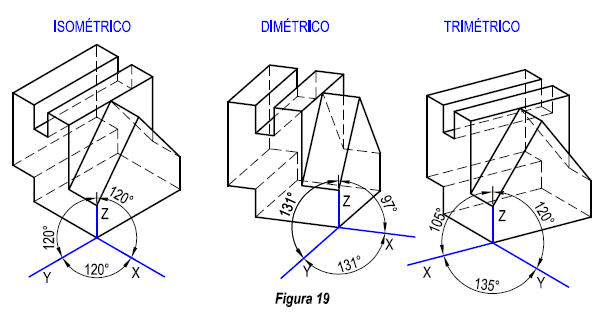
Para una mayor comprensión de lo expuesto, se detalla en la figura 19, una misma figura representada en los tres sistemas de representación..