| Rotulación Y Formatos | Croquización | Acotación | Sistemas de Acotación | Conicidad |
|---|---|---|---|---|
| Cortes y Secciones | Roscas- Acotación | Elementos de Unión | Signos Superficiales | Planos de Conjunto |
1. Conicidad La conicidad o adelgazamiento, es el aumento o disminución del diámetro por cada mm. de altura. Si placamos el teorema de Thales en la figura 43 B, tendremos que: 1/X = D/L, siendo: X = altura que debería tener el cono para que el diámetro D, adelgazase hasta convertirse en 1 mm. L= Longitud del cono.
Conicidad = diámetro del cono/altura = D/L
Utilizaremos las expresiones de conicidad para expresar piezas cónicas y adelgazamiento para piezas que no sean de revolución. Si se trata de un tronco de cono; definimos la conicidad como la relación que hay entre la diferencia de diámetros y su longitud. UNE 1-22.
Conicidad= (D-d)/L
2. Inclinación. La inclinación la definiremos como el cociente entre la diferencia entre sus radios y la longitud de un elemento cónico.
Inclinación= (D⁄2-d⁄2)/L = (D-d)/2L
Para expresar la conicidad o inclinación, usaremos los símbolos de la figura 43 A, seguido de una fracción que exprese su valor y orientados en el sentido según la conicidad o inclinación.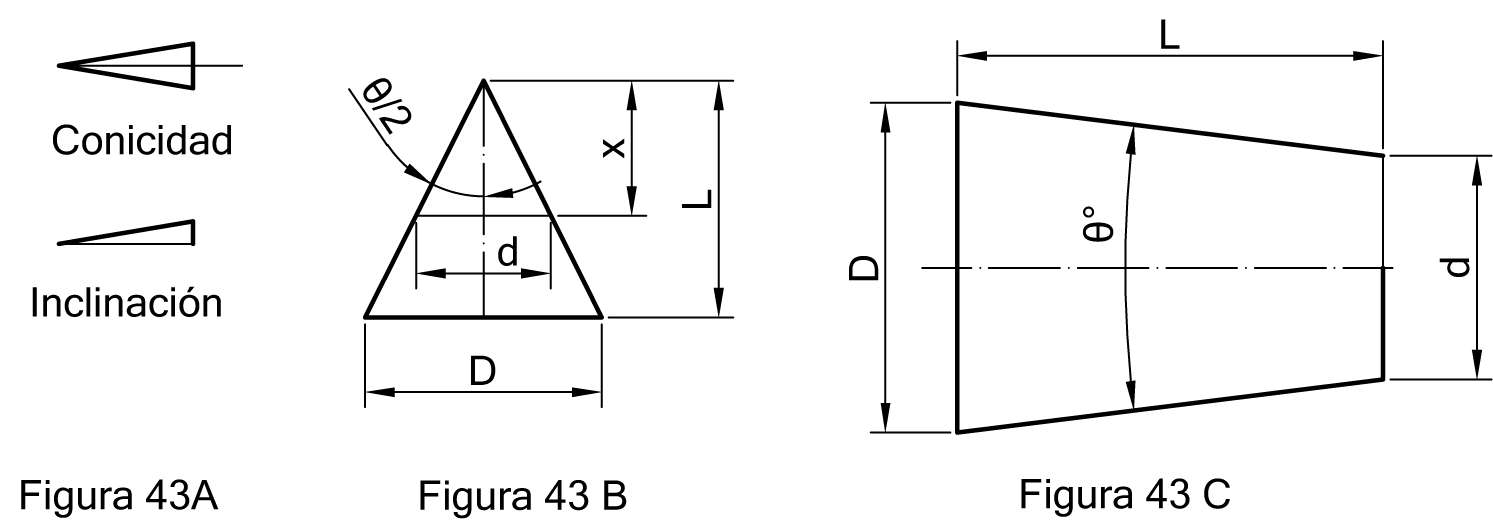
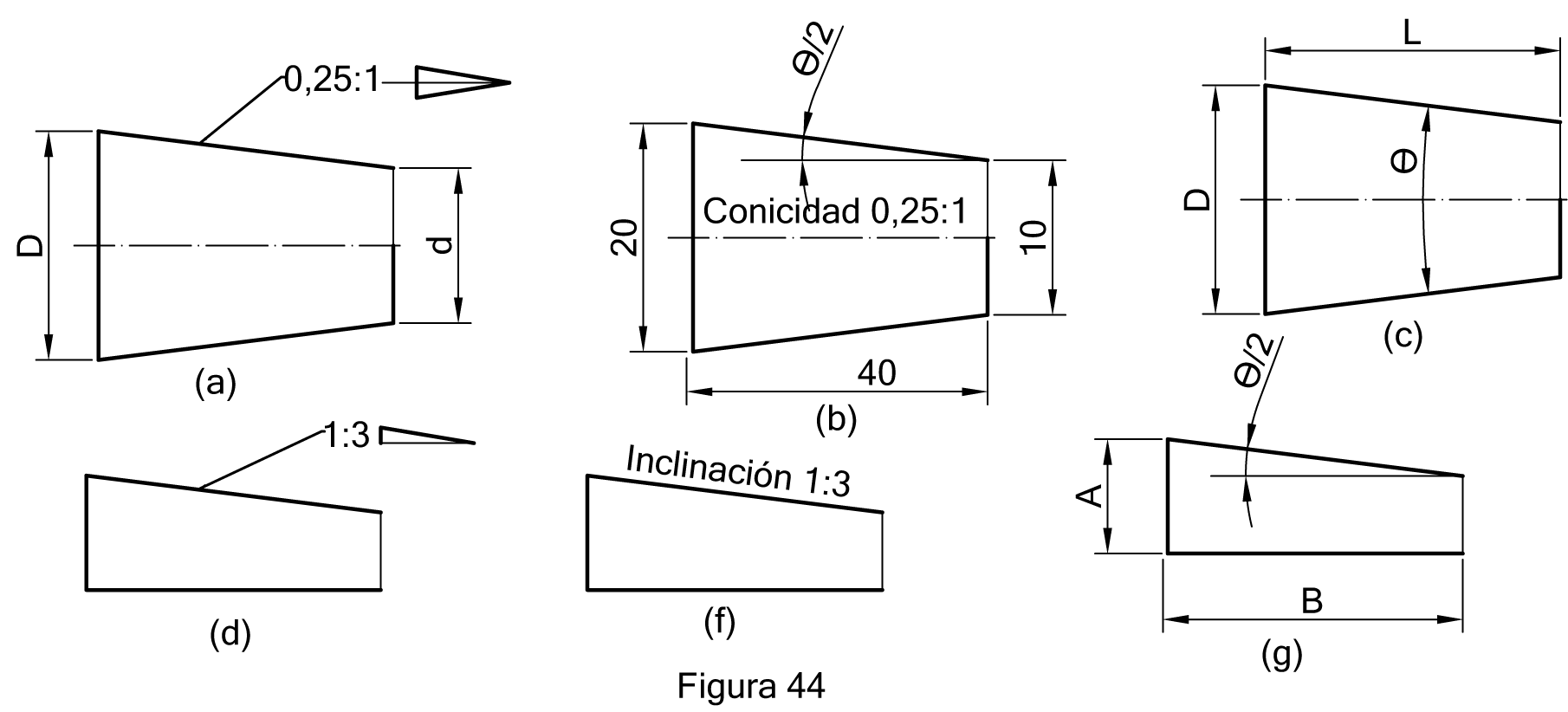
La piezas cónicas están fabricadas en tornos, por tanto será necesario conocer el ángulo de conicidad o inclinación, cuyo valor será la mitad del ángulo del cono Ɵ/2. Figura 44 b. Como podemos observar en dicha figura la generatriz del cono y una paralela al eje, forman un triángulo rectángulo nos determina la inclinación del mismo, en el que: un cateto es D-d, otro la longitud del cono L, y Ɵ/2 el ángulo que forman. De la figura se deduce que:
Inclinación = (D-d)/2L=(tang Θ)⁄2
Por ejemplo en la figura 43C, siendo. D= 20, d = 10 y L = 40, la conicidad valdría:
Conicidad = (D-d)/L=(20-10)/40=10/40=1/4
Para la inclinación tendríamos: Inclinación = (20-10)/(2×40)=10/80=0,125 Siendo la tang θ⁄2=1/8=7º 12» 50″
Ángulo que deberá ser expresado en el dibujo. Esta conicidad se expresaría de la forma siguiente 0,125:1, 1/8 o 7º 1’ 50” y se acotaría paralelo al eje de simetría.
En la figura 44, pueden verse algunos ejemplos de acotación de conicidades e inclinaciones.