| Utiles | Trazados Fund. | Triángulos | Polígonos | Igualdad y Semejanza |
|---|---|---|---|---|
| Potencia. Eje Radical | Homologia y Afinidad | Tangencias | Enlaces, Óvalos, Espirales | Cónicas |
1) Elipse.
1.1. Generalidades
Se llama elipse al lugar geométrico de los puntos de un plano tales que la suma de las distancias a dos puntos fijos del mismo plano llamados focos c , es constante e igual 2a. Siendo a el valor del eje mayor. y las rectas que los unen el punto de la elipse P radio vectores, que representaremos por r y r’. Entre ellos existe la siguiente relación r + r’ = 2a. Fig. 205
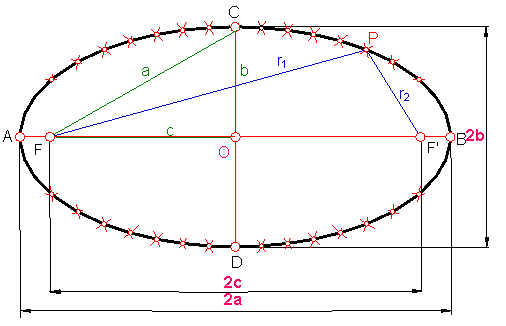
Fig. 205
La elipse tiene dos ejes perpendiculares que se cortan en su punto medio O. El eje mayor los representaremos por 2a, y el menor por 2b. A la distancia focal la llamaremos 2c.
Los semiejes los representaremos a, b y c, y entre ellos existe la relación siguiente: a2 = b2 + c2.
Para comprobarlo bastará con aplicar la propiedad que la define:
AF + AF’ = 2a. Como, AF = BF’ tendremos que AF’ + BF’ = 2a.
1.2. Circunferencia principal Cp
La circunferencia principal Cp tiene por centro el de la elipse y radio a. Fig. 206.
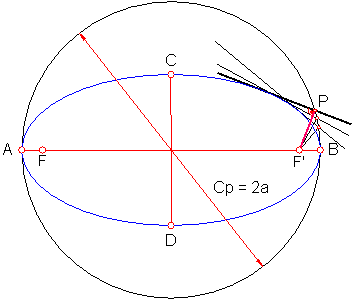
Fig. 206
Se define como el lugar geométrico de los pies de las perpendiculares trazadas por los focos a las tangentes a la curva.
1.3. Circunferencia Focal Cf
Tiene como centros los focos F y F’ y como radio el eje mayor 2a. Tendremos dos circunferencias focales. Fig. 207.
Se define como el lugar geométrico de los puntos simétricos del foco con respecto a las tangentes a la curva.
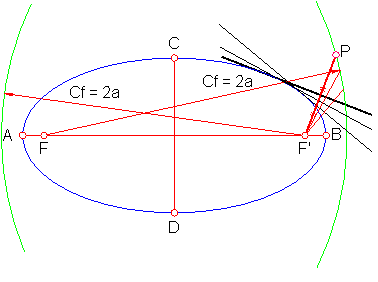
Fig. 207
1.4. Construcción de la elipse
a) Método del jardinero
Este método aplica la propiedad de la curva r + r’ = 2ª. Y se aplica principalmente para construcciones en jardineria.
Se coloca un clavo o chicheta en cada foco, y se fijan con ello los extremos de un hilo de longitud 2a. Con lápiz o punzon se tensa y se describe la curva.
b) Dado el eje mayor y el menor, construir la elipse por medio de puntos. Fig. 208.
Para su construcción nos basamos en la propiedad de la elipse r + r’ = 2ª
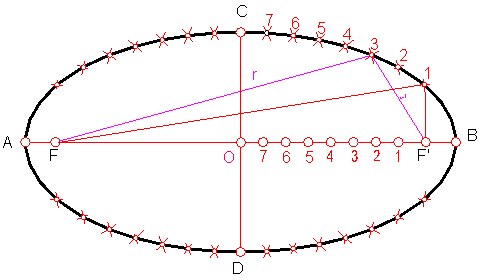
Fig. 208
Una vez fijados los ejes y los focos, elegimos en el semieje O F’ un número de divisiones por ejemplo de 1 a 7.
Con la distancia de A a la división 1 y haciendo centro en F trazamos un arco.
Con la distancia de B a 1 y haciendo centro en F’, trazamos un arco que cortará al anterior en el punto 1’.
Repitiendo la operación para los distintos puntos obtendremos la elipse.
En su construcción hay que tener en cuenta que la curva es simétrica con respecto a dos ejes.
a) Dado el eje mayor de la elipse y el menor, construir la curva por medio de haces proyectivos. Fig. 209.
En primer lugar construimos el paralelogramo ABCD.
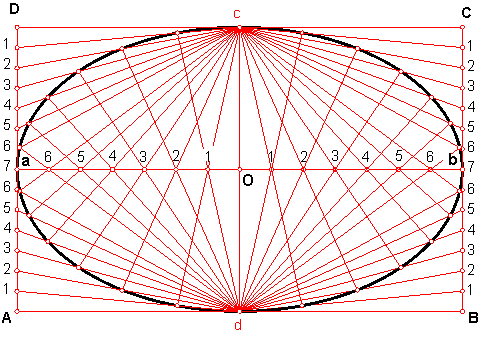
Dividimos el semieje O b, en un número de partes iguales, por ejemplo siete.
Dividimos en el mismo número, el lado menor bC.
Se unen las divisiones entre si.
Repetimos la operación hasta obtener la curva completa.
b) Dados los diámetros conjugados, construir la elipse por haces proyectivos. Fig. 210.
El procedimiento es similar al visto con anterioridad.
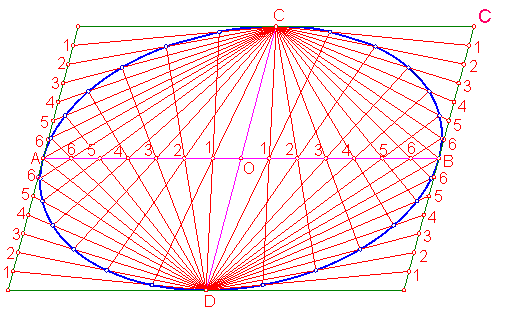
Fig. 210
c) Dado el eje mayor de la elipse y el menor, construir la curva por medio de afinidad. Fig. 211.
Aplicaremos la relación de afinidad entre circunferencia y elipse.
Trazamos los ejes AB y CD
Trazamos dos circunferencias de radio eje mayor AB y menor CD.
Dividimos una de las circunferencias en un numero de partes iguales.
Unimos dichas divisiones con el centro O.
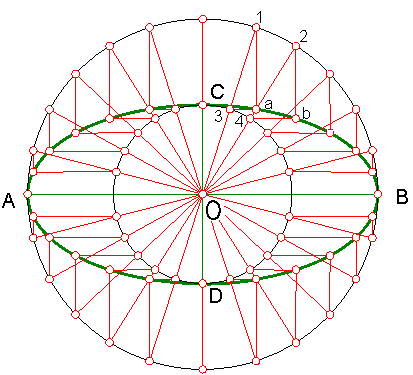
Fig. 211
Por el punto de división 1 trazamos una paralela eje menor. Y por el punto de división
3 otra paralela al eje mayor. Ambas se cortan en a, primer punto de la curva.
Repetimos la operación tantas veces como puntos hallamos elegido.
La hipérbola es una curva abierta de dos ramas y se define como; el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos llamados focos es constante e igual al eje mayor. (r1 – r2 = 2a). Fig. 212.
La curva es simétrica, tiene dos ejes que se cortan en su punto medio y son ortogonales.
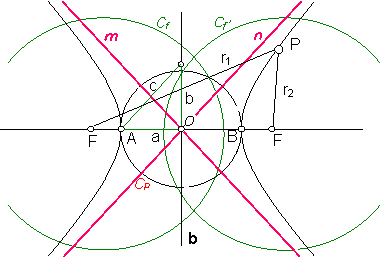
Fig. 212
La hipérbola tiene un eje real AB = 2a. Y un eje imaginario: 2b. La distancia focal la representaremos por: F F’ = 2c
Entre el eje real, eje imaginario y distancia focal existe la siguiente relación.
c2 = a2 + b2
Considerando un punto cualquiera P en la hipérbola, se denomina radio vectores a la distancia del punto a cada uno de los focos. Debe cumplirse que: r1 – r2 = 2a
Asíntotas: son las rectas tangentes a la curva en el infinito.
1.5.1. Construcción de la Hiperbola
a) Trazar la hipérbola por radio vectores dado el eje real y el eje imaginario. Fig. 213.
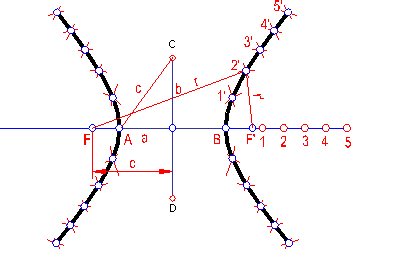
Fig. 213
Debemos de hallar el valor de la distancia focal. Para ello tendremos en cuenta la propiedad de la hipérbola en la que c2 = a2 + b2. Por tanto construiremos un triángulo rectángulo en el que un cateto sea el semieje real y el otro el imaginario. Fig. 214.
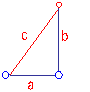
Fig. 214
Teniendo en cuenta otra propiedad de la hipérbola en la que la diferencia de los radios vectores es igual al eje real r – r’ = 2a, hallaremos los distintos puntos de la curva.
Tomamos un número determinado de puntos a la derecha de uno de los focos, por ejemplo cinco. Seguidamente con la distancia desde A al punto 1 y haciendo centro en el foco F se traza un arco. A continuación con la distancia de B al mismo punto (1) y haciendo centro F’ se traza otro arco que cortará al anterior en el punto 1’. De la misma forma se repite par el resto de los puntos.
a) Trazar la hipérbola por haces proyectivos. Fig. 215.
Se traza un punto cualquiera de la hipérbola el punto P por ejemplo.
Construimos el rectángulo B M P’ N.
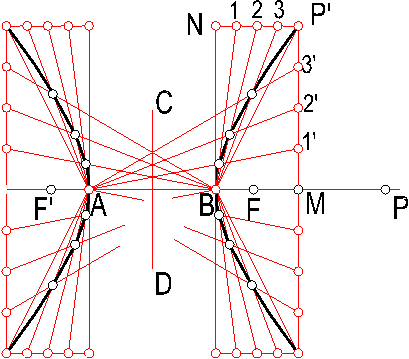
Fig. 215
Dividimos MP’ y BN, en el mismo número de partes iguales.
El resto de la construcción se deduce de la figura.
b) Trazar la hipérbola por tangentes a la curva. Fig. 216.
Para su construcción nos basaremos en la propiedad de la circunferencia principal que se define como el lugar geométrico de los pies de las perpendiculares trazadas por el foco a las tangentes a la curva.
Partimos del eje real AB y los focos F-F’.
Trazamos la circunferencia principal Cp.
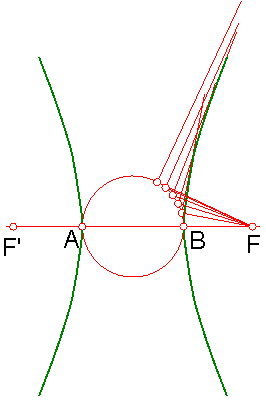
Fig. 216
Se toman en la Cp una serie de divisiones, que unimos con el foco F.
Trazamos los pies de las perpendiculares de las rectas anteriores. Finalizamos trazando la curva.
DEFINICIÓN: Es una curva plana, abierta, de una sola rama; y se define como el lugar geométrico de los puntos que equidistan del foco y de la directriz FP = PF’. Fig. 217.
Eje de la parábola e: es la recta perpendicular a la directriz, que pasa por el foco.
Parámetro FP: Es la longitud de la cuerda que es perpendicular al eje en el foco p.
Vértice V: Es un punto que equidista de la directriz y del foco. Su distancia a cada uno de ellos es p/2, es decir la mitad del parámetro.
Radios vectores: Segmentos que distan del foco y de la directriz r y r’ .
Circunferencia principal: Es la recta tangente a la curva en el vértice.
Circunferencias focales: Es la recta directriz. En este caso de radio infinito.
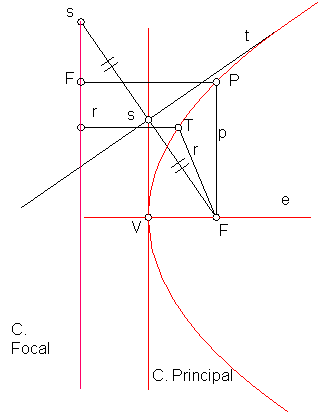
Fig. 217
La proyección del foco sobre una tangente está en la circunferencia principal
El punto simétrico de F, respecto de una tangente, está en la directriz.
1.6.1. Construcción de la Parábola
a) Construcción de la parábola por radio vectores. Fig. 218.

Fig. 218
A partir de V se toman un número de partes iguales, tantas como puntos deseemos obtener, y trazamos perpendiculares al eje.
Teniendo en cuenta la propiedad de la parábola r = r’, se toman las distancias desde la directriz a cada división y haciendo centro en el foco, cortamos a cada una de ellas, obteniendo los diferentes puntos de la curva.
b) Construcción de la parábola por puntos, por medio haces proyectivos. Fig. 219.
Hallamos un punto cualquiera de la parábola P.
Construimos el rectángulo P-P’-6-6’.
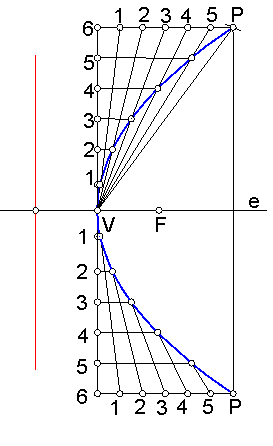
Fig. 219
Dividimos P-6, en un mismo número de partes iguales, que unimos con V.
Dividimos V-6 en el mismo número de partes y trazamos paralela al eje.
Las rectas anteriores nos determinaran los puntos de la curva.
c) Construcción de la parábola por puntos, a partir de la circunferencia principal. Fig. 220.
Nos basamos de nuevo en la propiedad de la circunferencia principal.
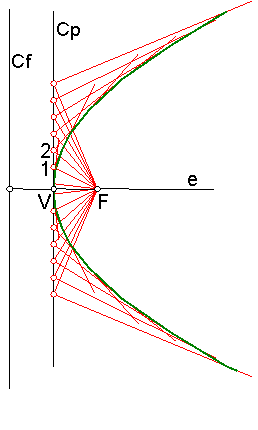
Fig. 220
Tomamos en la circunferencia principal Cp una
serie de divisiones.
Unimos cada una de las divisiones con el foco F, y
trazamos las perpendiculares 1,2,…….
Las rectas anteriores serán sucesivamente tangentes a
la parábola.
El otro ala de la curva será simétrico.


