| Utiles | Trazados Fund. | Triángulos | Polígonos | Igualdad y Semejanza |
|---|---|---|---|---|
| Potencia. Eje Radical | Homologia y Afinidad | Tangencias | Enlaces, Óvalos, Espirales | Cónicas |
Se denomina enlace o empalme de dos líneas, a la continuidad en el trazado conseguida por medio de alguno de los procedimientos que se han visto con anterioridad. Se fundamentan exclusivamente en los casos de tangencias y su utilización tiene aplicación en los trazados industriales. Seguidamente se realizaran algunos de ellos.
a) Empalme de dos rectas paralelas dado el punto de arranque T en una de ellas.
Sean las rectas r y s, y el punto de arranque T. Fig. 189.
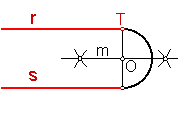
Fig. 189
La perpendicular a dichas rectas en el punto T, nos fijará en dentro de la solución.
Siendo O, la mediatriz de dicho segmento.
b) Empalme de dos rectas concurrentes por un arco de radio R. Fig. 190.
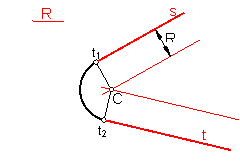
Fig. 190
Sean las rectas r y s, y R el radio dado.
Las paralelas a r y s a la distancia R, se cortarán en el punto C, centro de la solución.
El punto de tangencia se hallará mediante las perpendiculares Ct1 y Ct2.
c) Empalme de dos rectas incidentes por dos arcos de sentido contrarios conocidos los puntos de arranque T1 y T2 y el radio de r de una de ellas. Fig. 191.
Sean las rectas r y s, el radio de la solución R y los punto de arranque T1 y T2.
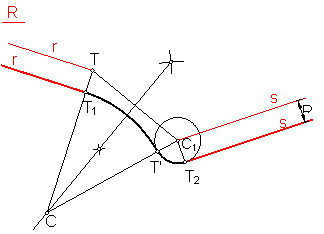
Fig. 191
Trazamos dos rectas r’ y s’ paralelas a r y s, a la distancia dada R.
Trazamos la circunferencia de centro C2 y radio R El centro C2, estará en la perpendicular TT1, con la mediatriz de T C1.
D) Empalme de recta y circunferencia dado el punto de arranque en la recta. Fig. 192.
Sea la recta r y la circunferencia de radio R, siendo T el punto de arranque.
Trazamos una paralela r’ a r a la distancia R.
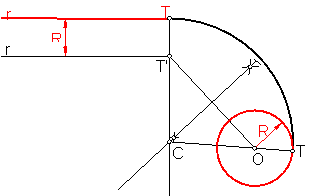
Fig. 192
El centro C1 estará en la perpendicular TT’ con la Mediatriz T’ O.
El ovalo es una figura cerrada formada por arcos de circunferencia que tiene una gran semejanza con la elipse. Tiene dos ejes perpendiculares que se cortan en su punto medio. Su uso principal es la sustitución de las elipses en los trazados.
a) Óvalo de cuatro centros dado el eje menor CD. Fig. 193.
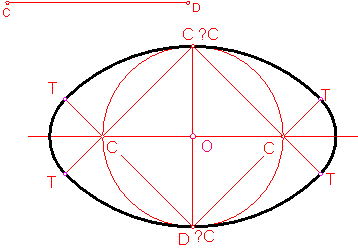
Trazamos la mediatriz del el eje menor.
Haciendo centro en O, trazamos una circunferencia que tenga por diámetro el eje menor.
Los centros de los arcos serán los puntos C1, C2…
b) Óvalo de cuatro centros dado el eje mayor AB.( primer procedimiento). Fig. 194.
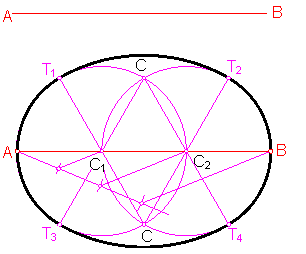
Fig. 194
Dividimos el eje mayor en tres partes iguales
Haciendo centro en C1 y C2, trazamos dos Circunferencias de radio 1/3 de AB.
Los centros serán los puntos C1, C2…
c) Óvalo de cuatro centros dado el eje mayor (segundo procedimiento). Fig. 195.
Sea el eje mayor AB.
Dividimos el eje AB en cuatro partes iguales, Obteniendo los centros C1 y C2..
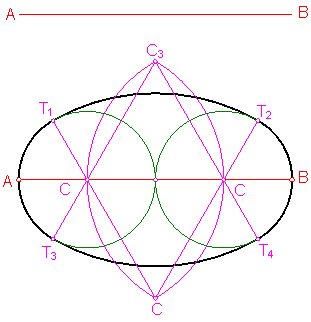
Fig. 195
Con centro en C1 y C2 y radio C1C2= AB/2, Se trazan dos arcos que determinan los centros C3 y C4,
Los puntos de tangencia T1, T2…. se obtendrán uniendo los centros hallados.
Como puede observarse en ambas figuras, el óvalo tiene curvaturas diferentes, aun siendo el eje mayor de igual medida.
C) Óvalo de cuatro centros dados los dos ejes.( primer procedimiento). Fig. 196.
Esta construcción es de bastante interés en el dibujo industrial por suplir en bastantes ocasiones a la elipse.
Son varios los procedimientos para su construcción, aunque solo se citarán los más usados.
Llevamos sobre la prolongación del eje menor, el valor del eje mayor. Punto a.
Unimos D con A.
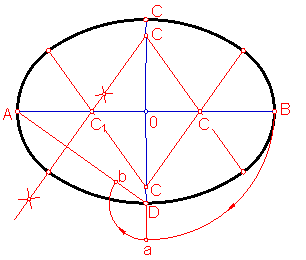
Fig. 196
Haciendo centro en el extremo del eje menor, punto D, trazamos un arco, punto b.
Trazamos la mediatriz del segmento bA.
Dicha mediatriz nos determina los centros C1 y C3. los otros dos serán simétricos.
Los puntos de tangencia se hallan trazando las rectas que unen todos los centros.
D) Óvalo de cuatro centros dados los dos ejes.( segundo procedimiento). Fig. 197.
Se construye el rectángulo formado por el eje mayo y menor AB y CD dados.
Dividimos el lado EH y FG en cuatro partes Iguales.
Unimos C con E y F así como D con G y H .
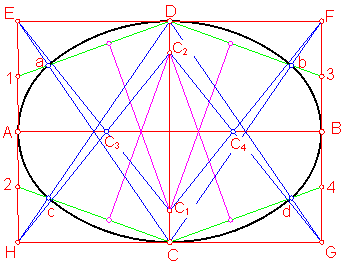
Fig. 197
Unimos el punto D con 1 y 3, así como C con 2 y 4 obteniendo los puntos de tangencia, a, b, c, d.
Trazamos la mediatriz de los segmentos aD, Bd, Cc, Cd. Obteniendo los centros C1 y C2.
Unimos C1 con E y con F, obteniendo los centros C3 y C4.
El ovoide presenta un solo eje de simetría y tiene la foma de un huevo, se construye también por arcos de circunferencia.
a) Ovoide dado el eje menor CD. Fig. 198.
Sea el eje menor CD
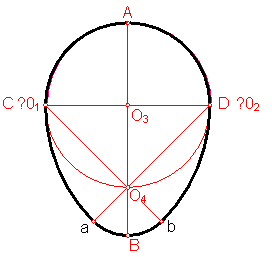
Fig. 198
Trazamos la mediatriz del eje CD dado.
Trazamos la circunferencia diámetro el eje menor.
Los puntos C y D Serán los centros O1 y O2.
Los Unimos con O4 y tendremos los puntos de tangencia a y b.
b) Ovoide dado el eje mayor AB. Fig. 199.
Dividimos el eje dado en seis partes Iguales.
Por la división 2 trazamos una perpendicular a la recta AB.
Sobre ella llevamos cuatro divisiones. Centros C3 y C4.
Con centro en la división 2 trazamos una semicircunferencia de radio 2 divisiones. Centro C1.
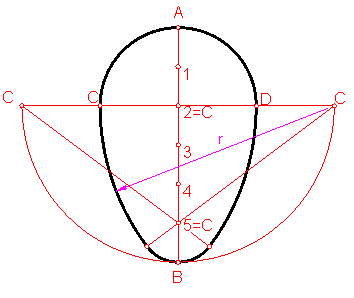
Fig. 199
El centro C4 estará en la división 5.
c) Ovoide común a dos circunferencias dadas. Fig. 200.
Sean las circunferencias de centro O1 y O2.
Tendremos que fijar un punto de contacto, p.e el T. Siendo su simétrico T’.
El problema se reduce a determinar las circunferencias tangentes a dos circunferencias conocido el punto de tangencia en una de ellas.
Lo ejecutaremos por dilataciones. Para ello restamos los radios de ambas circunferencias y con el resultado trazamos otra con centro en O1.
Bastará con trazar una circunferencia que pase por los puntos T1 y O2. Deshaciendo a continuación la dilatación.
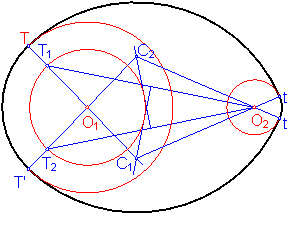
Fig. 200
Definimos la espiral como una curva generada por el doble movimiento de un punto; uno de
desplazamiento lineal sobre una recta y el otro angular.
Cada vuelta de 360º determina una espira. El conjunto de espiras forma la espiral.
Denominamos paso P a la distancia entre el principio y fin de una vuelta.
a) Falsa espiral de dos centros.
Tiene como base generadora el segmento AB que son los centros O1 y O2 de las curvas de 180º. Fig. 201.
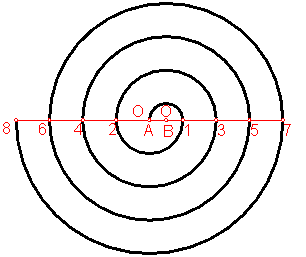
b) Falsa espiral basada en un triángulo.
Como puede observase cada espira está formada por tres arcos de circunferencia de 120º. Fig. 202.
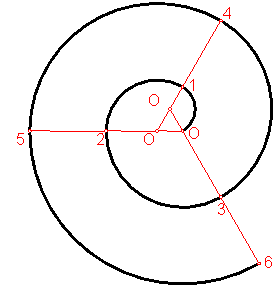
Fig. 202
Los centros de los arcos serán los vértices del triángulo.
Operaríamos de la misma forma si trabajásemos con otro polígono cualquiera.
c) Envolvente de la circunferencia.
Vamos a realizar el trazado por procedimiento aproximado, sustituyendo la circunferencia por un polígono circunscrito cualquiera. Cuantos mas lados tenga, mayor precisión obtendremos en la solución. Fg. 203.
En nuestro caso operaremos con un octógono.
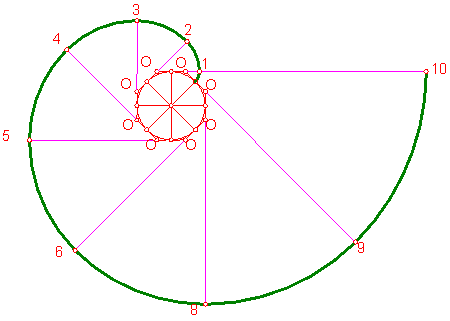
Fig. 203
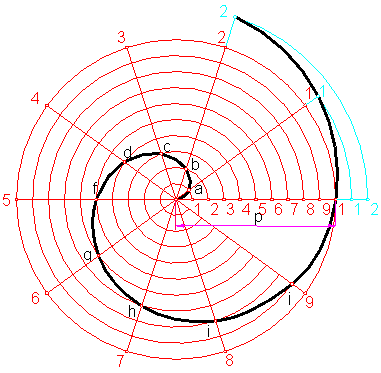
Fig. 204
d) Espiral de Arquímedes
Arquímedes de Siracusa (287-212a.C.), físico y matemático griego, describió la espiral de la forma
siguiente:
Si una línea recta que permanece fija en un extremo, se le hace girar en el plano con velocidad constante y, al mismo tiempo, se mueve un punto sobre la recta con velocidad constante comenzando por el extremo fijo, el punto describe en el plano una espiral»
Construcción:
Partimos del paso P, que dividimos en un número de partes iguales, cuantas más mejor, ya que su construcción es por puntos. Fig. 204.
Trazamos el circulo de radio P, que dividimos en el mismo número de partes.
La unión de los puntos a, b, c …., nos determinará la espiral.


