| Utiles | Trazados Fund. | Triángulos | Polígonos | Igualdad y Semejanza |
|---|---|---|---|---|
| Potencia. Eje Radical | Homologia y Afinidad | Tangencias | Enlaces, Óvalos, Espirales | Cónicas |
Potencia. Eje Radical.
Se llama potencia de un punto P con respecto a una circunferencia c al producto de
P A * P B = k, siendo A y B los punto de intersección de la circunferencia con una recta secante trazada desde P. Fig. 146.
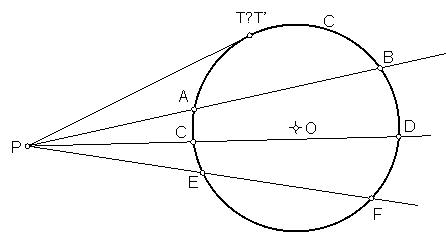
Fig. 146
Sea un punto P, y C, una circunferencia de centro O. Si desde el punto P, trazamos varias secantes a dicha circunferencia se verifica que:
P A * P B = P C *P D = P E * P F = k
donde k es la potencia del punto con respecto a la circunferencia. Siendo constante para cualquier recta secante o tangente que pase por P.
Las rectas tangentes a la circunferencia son un caso límite en ellas se cumple que :
P A * P B = P T * P T’ = P T2
De donde se deduce que el punto de tangencia de una recta que pase por el punto P a una circunferencia C, será la media proporcional de los segmentos PA y PB.
Si el punto P es exterior a la circunferencia, la potencia es positiva, ya que los segmentos PA y PB están orientados en el mismo sentido.
Si el punto está sobre la circunferencia, este coincide con uno de los puntos de intersección, la potencia será 0.
K = PA*PB = 0*PB = 0
Si el punto está dentro de la circunferencia, la potencia es negativa, ya que los segmentos PA y PB están orientados en sentido contrario.
PA *(-PB) = -k
Se denomina eje radical de dos circunferencias al lugar geométrico de los puntos del plano que tienen la misma potencia con respecto a ambas circunferencias. Fig. 147.
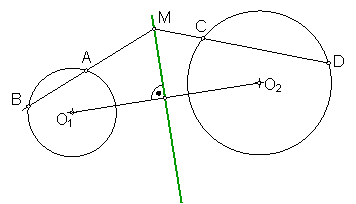
Fig. 147
MA * MB = MC *MD.
El eje radical será siempre perpendicular a la recta que une los centros de ambas circunferencias.
a) Eje radical de dos circunferencias tangentes. Fig. 148.
El eje radical de dos circunferencias tangentes se halla trazando la recta tangente común a ambas circunferencias.
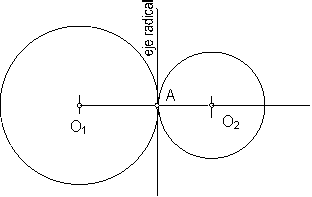
Fig. 148
a) El eje radical de dos circunferencias secantes. Fig.149
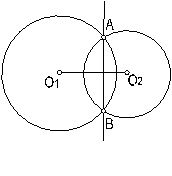
Fig. 149
El eje radical de dos circunferencias secante se halla uniendo los puntos de intersección de ambas circunferencias A y B,
d) Eje radical de dos circunferencias exteriores. Fig. 150.
Trazamos una circunferencia auxiliar cualquiera de centro O.
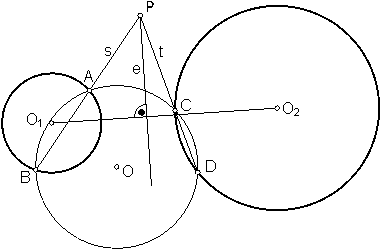
Fig. 150
Hallamos los ejes radicales s y t de dicha circunferencia con las otras dos.
Donde se cortan ambos ejes radicales, será un punto que tiene la misma potencia con respecto a ambas circunferencias. Trazando una perpendicular por este punto a la recta de unión de los centros tendremos la solución.
Se llama centro radical de tres circunferencias, cuyos centros no están alineados, al punto que tiene la misma potencia con respecto a ellas.
Sean tres circunferencias de centros O1, O2 y O3.
Trazamos una circunferencia auxiliar de centro O.
Se hallan los ejes radicales r, s. t, de dicha circunferencia con respecto a las otras tres, el punto de corte de ambas, será el centro radical. Fig. 151.

Fig. 151
d) Eje radical de dos circunferencias interiores. Fig. 152.
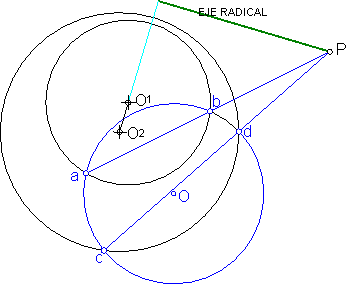
Fig. 152
Sean las circunferencias interiores de centros O1 y O2
Trazamos una circunferencia auxiliar de centro O.
Hallamos el eje radical entre la circunferencia auxiliar y la de centro O, recta ab.
Repetimos la operación con la de dentro O2, recta cd.
El punto donde se cortan ambas rectas tendrá la misma potencia con respecto a las dos circunferencias.
Una perpendicular a la recta que une los centros O1 y O2 nos dará la solución.
Si dibujamos las rectas comunes a dos C1 y C2 circunferencias podemos observar que el eje radical
pasa por su punto medio del segmento t1 y t2.. Fig. 153.
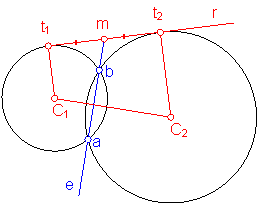
Fig. 153


