| Utiles | Trazados Fund. | Triángulos | Polígonos | Igualdad y Semejanza |
|---|---|---|---|---|
| Potencia. Eje Radical | Homologia y Afinidad | Tangencias | Enlaces, Óvalos, Espirales | Cónicas |
Construcción de formas poligonales
1) Definiciones y clasificación.
Línea poligonal A, B, C, D, es aquella formada por segmentos rectilíneos. Fig.49.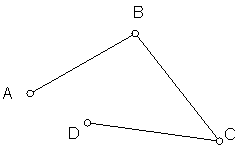
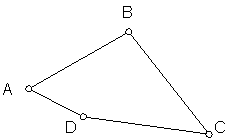
Fig. 50
Si los extremos de dicha línea se cierran, tendremos un polígono. Fig.50.
Lados son los segmentos que forman el polígono. Fig.51.
Vértices, son los puntos donde concurren dos lados.
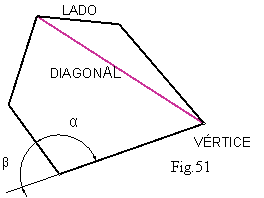
Fig. 50
Diagonal son segmentos que unen dos vértices no consecutivos Se llama Perímetro a la suma de todos sus lados.

Fig. 52
Ángulos interiores son los que forman dos lados consecutivos.
Ángulos exteriores son los complementarios de los anteriores
Polígonos convexo, es aquel que alargando un lado todos los vértices quedan a un lado de dicha recta. Fig.52.
Polígono cóncavo, es aquel que alargando alguno de sus lados los vértices quedan a ambos lados de la recta. Como puede
apreciarse el ángulo interior C es mayor que un llano. Fig.53.
Los polígonos pueden ser regulares e irregulares.

Fig. 53
De acuerdo con el número de lados los polígonos regulares
se clasifican de la forma siguiente:
| Nombre | Lados | Nombre | Lados |
| Triángulo | 3 | Eneágono | 9 |
| Cuadrado | 4 | Decágono | 10 |
| Pentágono | 5 | Undecágono Endecágono | 11 |
| Hexágono | 6 | Dodecágono | 12 |
| Heptágono | 7 | Pentadecágono | 15 |
| Octógono | 8 | Icoságono | 20 |
Se llama polígono equilátero, aquel que tiene todos sus lados iguales. Fig. 54.
Polígono equiángulo, es el que tiene todos sus ángulos iguales
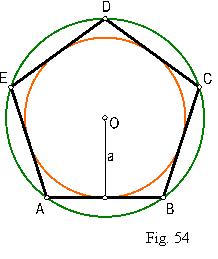
Fig. 54
Polígono regular, es el que cumple las dos condiciones
Teorema: Todo polígono regular es incriptible en una circunferencia y circunscriptible a otra que tiene el mismo centro.
Radio r del polígono regular, es el de la circunferencia circunscrita.
Apotema “a” de un polígono regular es el radio de la circunferencia Inscrita.
Ángulo central α, del polígono regular, es el formado por los radios que pasan por dos vértices consecutivos del polígono.
Teoremas: Los ángulos centrales de un polígono regular, son suplementarios de los interiores del mismo, e iguales a los exteriores. α + β = 180º.
Polígonos regular convexo, es aquel que se cierra después de recorrer una sola vez la circunferencia, pasando consecutivamente por todos sus vértices. Fig. 55.
Polígono regular estrellado, se cierra después de recorrer varias veces la circunferencia.

Fig. 55
Se llama triángulo a la porción de espacio del plano limitado por tres segmentos rectilíneos.
Lados de un triángulo son los segmentos que lo limitan.
El punto donde se cortan dos lados consecutivos se denomina, vértice, y se designa por una letra mayúscula.
Los lados se designan por la misma letra que el vértice opuesto, pero en minúscula.
Ángulo interior del triángulo, es el formado por dos lados consecutivos.
Ángulos exteriores, son los adyacentes de los interiores.
La suma de los lados internos de un triángulo es igual a dos rectos es decir 180º.
α + β + γ = 180º. Fig. 56.
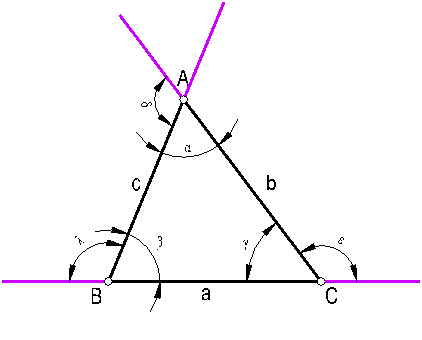
Fig. 56
El ángulo exterior de un triángulo, es igual a la suma de los dos interiores no adyacentes
ε = α + β.
A mayor ángulo se opone siempre mayo lado.
La suma de los lados de un triángulo siempre es mayor que el tercero.
Un lado de un triángulo es siempre mayor que la diferencia de los otros dos.
2.1. Nomenclatura y Clasificación de triángulos.
Para los vértices emplearemos letras mayúsculas, comenzando por el vértice superior y en sentido contrario a las agujas del reloj.
Los lados de un triángulo los nombraremos por letras minúsculas, de tal forma que p.e. al vértice A, le corresponda el lado a.
En ambos casos utilizaremos las primeras letras del abecedario.
Los triángulos atendiendo a sus ángulos los triángulos se clasifican en: rectángulos, acutángulos y obtusángulos.
Rectángulo: tiene un ángulo recto y dos agudos. Fig. 57.
Acutángulo: tiene tres ángulos agudos. Fig. 58.
Obtusángulo: tiene los tres ángulos obtusos. Fig. 59
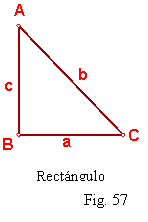
Fig. 57
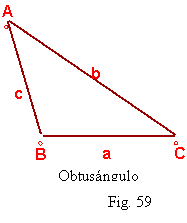
Fig. 59
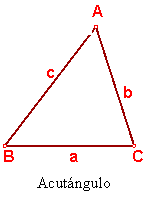
Fig. 58
Según la magnitud de su lados clasificamos los triángulos en:
Equilátero: Los tres lados iguales. Fig. 60
Isósceles: Dos lados iguales y uno desigual. Fig. 61
Escaleno: Todos sus lados desiguales. Fig. 62
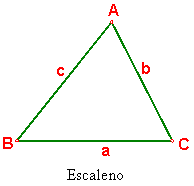
Fig. 62
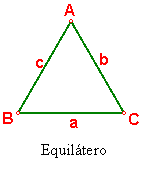
Fig. 60
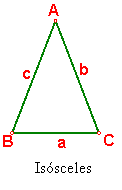
Fig. 61
2.2. Puntos notables de un triángulo.
Se llama mediana ma de triángulo, a la recta que une un vértice con el punto medio del lado opuesto. El punto donde se cortan las medianas de un triángulo se llama baricentro Bc.. Fig. 63.
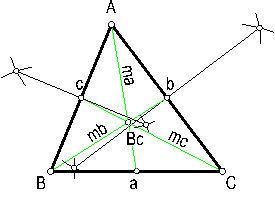
Fig. 63
Construcción : Hallamos la mediatriz de cada uno de los lados del triángulo.
Unimos cada vértice con el punto medio del lado opuesto hallado.
El punto de intersección de las medianas será el baricentro Bc. Fig. 63.
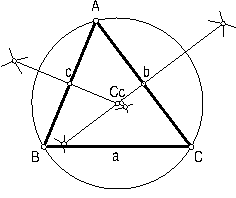
Fig. 64
Se llama circuncentro Cc de un triángulo, al punto de intersección de sus mediatrices de sus lados. Fig. 64.
El circuncentro equidista de sus vértices y es el centro de la circunferencia circunscrita.
Construcción: Hallamos las mediatrices de sus lados.
El punto de corte de las mediatrices Cc, será el circuncentro del triángulo y centro de la circunferencia circunscrita.
Se llama ortocentro Oc de un triángulo, al punto donde concurren las alturas del mismo. Fig. 65.
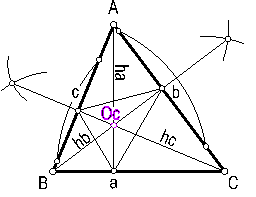
Fig. 65
Para su construcción: Bastará con trazar la perpendicular desde cada vértice al lado opuesto. El punto de corte será el ortocentro Oc.
La unión de los pies de las alturas formarán un triángulo que se llama Triángulo Órtico.
Se llama incetro Ic de triángulo, al punto de intersección de las bisectrices de sus ángulos. Fig. 66.
Para su construcción, bastará con trazar las bisectrices de dos de sus ángulos.
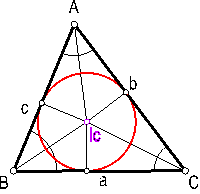
Fig. 66
El incentro equidista de sus tres lados y por ello es el centro de la circunferencia inscrita al triángulo.
Existen puntos exteriores que tienen la misma propiedad y que se denominan exincentros.
La circunferencia que es tangente a un lado y a las prolongaciones de los otros, se llama exinscrita.
2.3. Recta de Euler
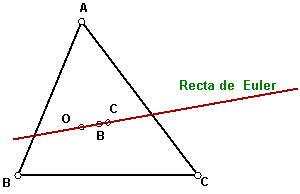
Fig. 67
Leonardo Euler ( 1707-1783), demostró que el baricentro, ortocentro y circuncentro de un
triángulo están en línea recta. A dicha recta se le llama Recta de Euler. Fig. 67.
Además se verifica que el baricentro esta situado entre el ortocentro y circuncentro y a doble distancia del primero que del segundo.
2.4. Construcción de triángulos
Para la construcción de un triángulo serán necesarios conocer tres datos, o bien un dato y dos condiciones o dos datos y una condición. Las condiciones pueden ser lados, ángulos o cualquier otra.
2.4.1. Triángulos equiláteros.
a) Trazado de un triángulo equilátero dado un lado. Fig. 68.
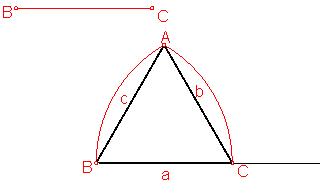
Fig. 68
Al ser los tres lados iguales, operaríamos de la forma siguiente:
Sobre una recta cualquiera, llevamos el lado BC.
Con centro en B y C trazamos arcos de radio BC, obteniendo el punto A. vértice buscado.
b) Trazado de un triángulo equilátero conociendo el radio r de la circunferencia circunscrita. Fig. 69.
Trazamos una circunferencia de radio r y centro O:
Con centro en m y radio r trazamos un arco que pase por O. Dicho corta a la circunferencia en BC.
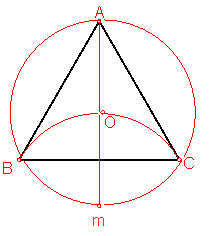
Fig. 69
Unimos A, B, y C, obteniendo el triángulo buscado
2.4.2. Triángulos isósceles
a) Trazado de un triángulo isósceles conociendo dos tres lados. Fig. 70.
Sean los lados a y b:
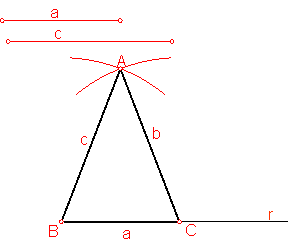
Fig. 70
Sobre una recta cualquiera r, llevamos el valor de a.
Haciendo centro en B y C y con el radio c, lado que se repite, trazamos dos arcos de circunferencia obteniendo el vértice A.
Uniendo A, B y C tendremos el triángulo.
b) Trazado de un triángulo isósceles dado el lado desigual y el ángulo opuesto. Fig. 71
Construimos el ángulo desigual A.
Hallamos la bisectriz de A.
Trazamos la mediatriz del segmento BC, obteniendo a/2.
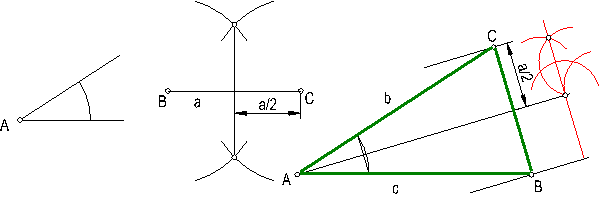
Fig. 71
Trazamos una perpendicular a la recta bisectriz en un punto cualquiera, y llevamos sobre ella a/2. Trazamos dos paralelas, y tenemos resuelto el problema.
c) Hallar el triángulo isósceles dado el ángulo desigual “ A “ y la suma del lado “ a “ y la altura ( a + h ). Fig. 72.
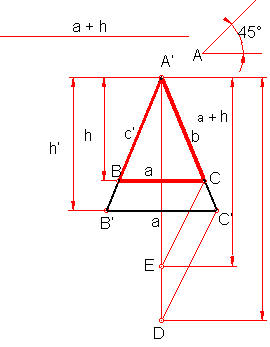
Fig. 72
Este ejercicio se resolverá por semejanza.
Como regla general todos los ejercicios que utilicemos para su construcción este método, partiremos de un triángulo cualquiera, ya que todos ellos serán semejantes.
Se construye un triángulo isósceles cualquiera A’, B’, C’ con el ángulo desigual en “A”.
Se prolonga la altura de dicho triángulo.
Se lleva sobre dicha recta la suma del lado a’ y su altura correspondiente h’.
Se une el punto D con el vértice C’.
Sobre la prolongación de la altura se lleva a + h.
Por el punto E se traza una recta paralela a DC’, resultando el vértice C que completa el ejercicio.
2.4.3. Triángulos escalenos
a) Trazado de un triángulo isósceles dado el lado igual y el ángulo desigual. Fig. 73.
Sea el ángulo A y el lado c:
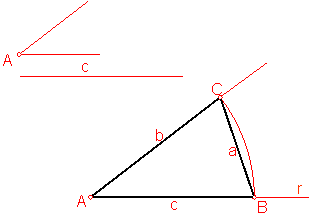
Fig. 73
Sobre una recta r cualquiera llevamos el valor de ángulo A.
Haciendo centro en A y con radio el valor del lado trazamos un arco de circunferencia que nos determinan los vértices B y C.
Con la unión de A, B y C, tendremos la solución.
b) Trazado de un triángulo escaleno, conociendo sus tres lados. Fig. 74.
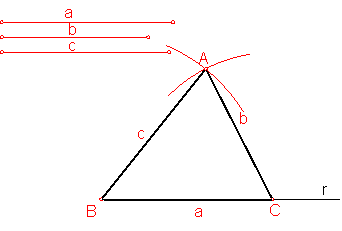
Fig. 74
Sean los lados a, b, c:
Sobre una recta r, llevamos el valor del lado a.
Tomando con el compás el valor del lado c, se traza un arco haciendo centro en B.
Se realiza la misma operación con el lado b, haciendo centro en C.
La intersección de ambos arcos de circunferencia determina el vértice A, que uniendo con B y C nos da el triángulo buscado.
c) Trazado de un triángulo escaleno dado dos lados y el ángulo que forman. Fig. 75.
Sean los lados a y c y el ángulo comprendido B:
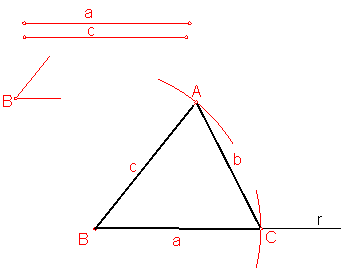
Fig. 76
Sobre una recta r cualquiera construimos el ángulo B dado.
Con centro en B y radio el valor de los lados, trazamos dos arcos, que determinan los vértices A y B.
La unión de A, B, y C, nos da la solución.
d) Triángulo escaleno conociendo dos lados a y c y el ángulo opuesto a uno de ellos B. Fig. 76.
Sea el ángulo A y los lados a y c:
Sobre una recta r, y en un punto de ella construimos el ángulo A.
Llevamos a partir de A el lado c.
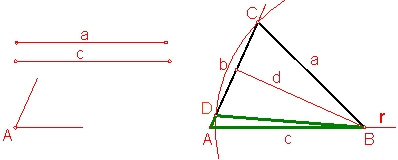
Fig. 76
Con centro en B y radio el lado a trazamos un arco que determina el vértice C y D. El ejercicio tendrá dos soluciones.
Según la distancia d, el ejercicio puede tener una solución, dos o cero.
e) Por medio del Arco capaz. Trazar un triángulo escaleno, conociendo su base, el ángulo opuesto y otro lado. Fig. 77.
La forma mas sencilla para la construcción de un triángulo cuando se conoce un lado y el vértice opuesto al mismo, es el empleo del arco capaz.
Sobre el lado a construimos el ángulo dado A.
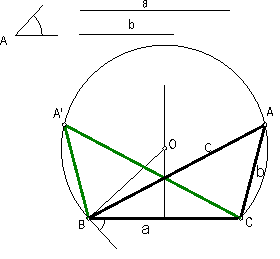
Fig. 77
Por el extremo de B, trazamos una perpendicular hasta que corte a la mediatriz del lado a.
Con centro en O, trazamos el arco capaz.
Haciendo centro en B y C trazamos dos arcos que cortan a la circunferencia, en los puntos A y A’, soluciones buscadas.
Se une el punto D con el vértice C’.
Sobre la prolongación de la altura se lleva a + h.
Por el punto E se traza una recta paralela a DC’, resultando el vértice C que completa el ejercicio
f) Construir un triángulo escaleno, conociendo un lado a, el ángulo opuesto y la altura ha, correspondiente a dicho lado. Fig. 78.
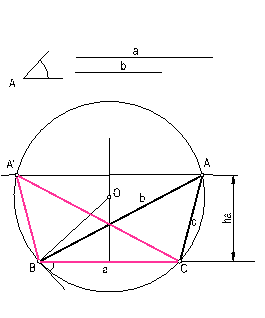
Fig. 78
El ejercicio es similar al visto anteriormente. Una vez resuelto el arco capaz, trazaremos una paralela al lado a con el valor de ha. Esta cortará a la circunferencia en los puntos A y A’, que unidos con B y C, obtendremos las soluciones.
a) Construcción de un triángulo escaleno, conociendo el lado a, el ángulo opuesto A = 60º y la mediana ma. Fig. 79.
Construimos el arco capaz llevando en el segmento a partir del extremo B, el ángulo de 30º, diferencia entre 90-60.
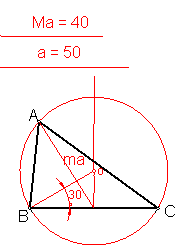
Fig. 79
El siguiente paso será hacer centro en la mitad del lado a, y con el valor de la mediana ma, trazar un arco que cortará a la circunferencia en el vértice buscado A.
2.4.4. Triángulos rectángulos
La nomenclatura de estos triángulos será similar a los vistos con anterioridad, con la única salvedad de comenzar la designación por el ángulo recto, al que llamaremos A.
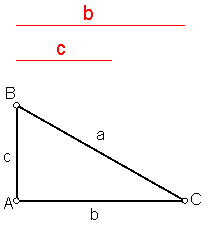
Fig. 80
b)Construir un triángulo rectángulo conociendo dos catetos b y c. Fig. 80.
Para su construcción se requieren tres datos, en este caso por ser un triángulo rectángulo, los dos catetos y el ángulo que forman de 90º.
Para su construcción levantamos en uno de los extremos del cateto b una perpendicular.
Sobre la perpendicular llevamos el cateto c. La unión de B y C nos dará la solución.
c) Construcción de un triángulo rectángulo, conociendo un cateto y el ángulo agudo. Fig. 81.
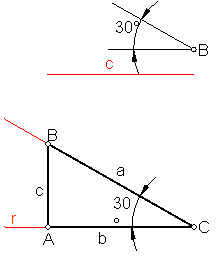
Fig. 81
Sobre una recta cualquiera r, llevamos el cateto b en uno de sus extremos, p.e. C construimos el ángulo dado.
Por el extremo A, levantamos una perpendicular que determina el vértice B.
d) Construcción de un triángulo rectángulo, conociendo un cateto y la hipotenusa. Fig. 82.
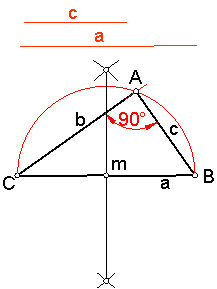
Fig. 82
Hallamos la mediatriz m de la hipotenusa.
Haciendo centro m, trazamos una semicircunferencia.
Con el compás tomamos el valor de lado c, y haciendo centro en B, trazamos un arco que determina el vértice A.
La unión de A, B, C nos dará el triángulo buscado.
Obsérvese que la construcción está basa en el Arco Capaz .


