- 1. Representación de cuerpos.
Para la representación de cuerpos, se hará preciso conseguir las proyecciones horizontal y vertical de todos sus vértices, ya que a partir de ellos quedarán delimitados las proyecciones de las aristas, y por consiguiente sus caras.
Un cuerpo podrá ocupar en el espacio diversas posiciones, pero teniendo en cuenta que el estudio se realiza con miras prácticos, los situaremos en posiciones convenientes.
Es de vital importancia en la presentación de cuerpos, la determinación de las aristas visibles y ocultas. Para ello tendremos en cuanta las consideraciones siguientes.
a) Se llama contorno apararen te de una proyección, a la forma poligonal o curva de la silueta. Estos resultan siempre visibles.
b) Serán visibles en proyección horizontal, las aristas y vértices que estén más alejados de la charnela en proyección vertical. Resultan ocultas en proyección horizontal, las aristas y vértices que en el vertical estén más próximas a la charnela.
c) Serán visibles verticalmente aquellas aristas y vértices, que horizontalmente resulten las alejadas de la charnela y por tanto más próximas al observador.
1.1. Hallar la proyección de un prisma triangular dado por su base Mo, No, Po, apoyada en un plano dado por su traza αo. Sabiendo que el vértice P, tienen una cota de 4 cm. Siendo la altura del prisma 5 cm. Figura 58.
1) Trazamos por el punto Po, una perpendicular a la traza αo que utilizamos como charnela.
2) En un punto cualquiera de la charnela trazamos la perpendicular h.
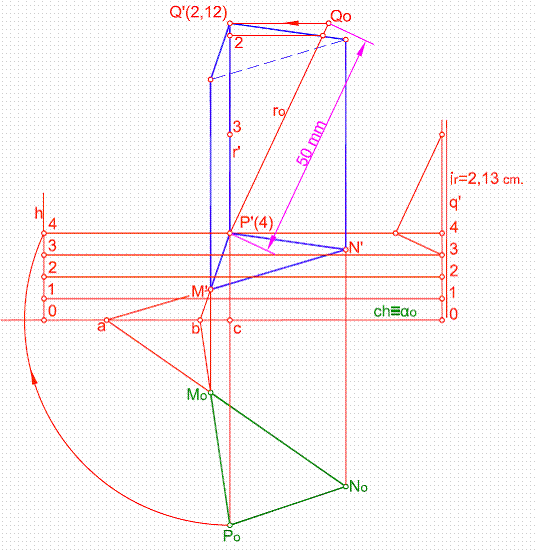
Figura 58
3) Haciendo centro en c, y con la distancia cPo, trazamos un arco que corte a h en el punto 4.
4) Graduamos dicha recta, obteniendo la graduación del plano q’.
5) Por el punto P’(4), trazamos un recta r’ perpendicular al plano, hallando previamente el intervalo de la recta ir.
6) Abatimos el plano proyectante que contiene a r’, recta P’ Qo,
7) A partir de P’(4) y sobre ro, llevamos en verdadera magnitud la altura del prisma 5 cm. Obteniendo el punto Qo
8) Deshacemos el abatimiento punto Q’ (2,12), y obtenemos la altura del prima en proyección.
9) Llevamos la altura en proyección sobre los vértices M’ y N’, que uniendo nos determina el prisma buscado.
1.2. Hallar la proyección de un cono apoyado en un plano oblicuo de l.m.p. q’. Conociendo su base la traza αo y el centro de la misma Oo de cota 3,5 cm. Figura 59.
1) Dividimos la circunferencia de la base en un número de partes iguales, por ejemplo 8.
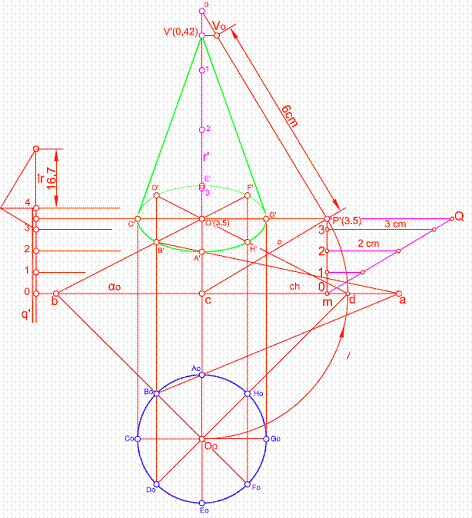
Figura 59
2) Trazamos una perpendicular a la charnela αo por Oo, que corta a esta en el punto c.
3) Trazamos una perpendicular a la charnela en un punto cualquiera de ella, por ejemplo en m.
4) Haciendo centro en c, y con radio cOo, trazamos un arco que corte a la perpendicular por m en punto P’(3,5).
5) Graduamos el plano. Para ello trazamos una perpendicular por P’, y sobre ella llevados la cota de 3,5 cm, obteniendo el punto Q.
6) Unimos Q con m y trazando paralelas a la recta P’m, con valor de 3, 2 y 1 cm,, obtenemos la graduación del plano.
7) Trazamos una recta r’ perpendicular al plano por O’, previamente hallamos el intervalo de la recta ir. Graduamos la recta.
8) Abatimos el plano proyectante O’ 0. El resto del ejercicio es similar visto anteriormente.
1.3. Hallar la proyección de un prisma de base triangular regular inscrito en una circunferencia de 45 mm de diámetro y vértices Ao, Bo, Co. Su altura es 35 mm, apoyado en un plano αo de l.m.p. q’. Su centro se encuentra en la recta r’ dada y tiene una cota de 2 cm. El vértice C’ tiene de cota 0,67. Seguidamente hallar la sección en proyección y verdadera magnitud que produce el plano β de l.m.p. v’.Figura 60.
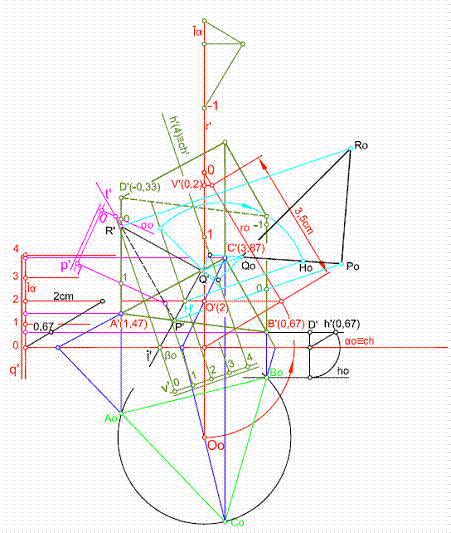
Figura 60
1) Trazamos un plano α perpendicular a r’ de l.m.p. q’, Hallando previamente el intervalo del plano iα.
2) Con el intervalo iα. A partir de Q’(2), graduamos el plano
3) Hallamos el centro del prisma Oo, como se ha visto en los ejercicios anteriores
4) Hallamos la horizontal de plano h’(0,67). Elegimos un punto cualquiera D’ y lo abatimos.
5) Construimos el triángulo Ao, Bo, Co.
6) Por afinidad hallamos la proyección A’, B’, C’, calculando a continuación el valor de sus cotas.
7) Abatimos el plano proyectante O’(2)-O, que pasa por la recta r’ y llevamos sobre ro el valor de la altura del prisma 3,5 cm. obteniendo el centro V’(0,2).
8) Sobre los vértices A’, B’, C’, llevamos la distancia O’V’, completando el prisma
9) A continuación vamos hallar la sección que produce el plano β de l.m.p v’ en el prisma. Como el prisma se encuentra apoyado en el plano de l.m.p. q’, hallaremos la intersección de este con v’, recta i’.
10) Haremos contener a la arista D’ en un plano cualquiera σ de l.m.p. p’, hallando a continuación su intersección con v’, recta t’.
11) La recta i’ corta a la arista A’D’ en R’, que unido con P’ y Q’, nos da la sección en proyección.
12) Como la sección se encuentra en el plano v’, elegiremos como charnela una de sus horizontales de plano, por ejemplo la h’(4). El resto del abatimiento se ha visto con anterioridad.
“Ir al ïndice”


