- 1. Ángulos
1.1. Ángulos de dos rectas.
Bastará con abatir el plano β que contiene a las rectas. Las rectas abatidas nos determinarán el ángulo α. Figura 53.
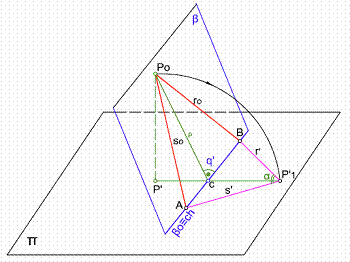
Figura 53
Sean las rectas ro y so en el espacio que se cortan en el punto Po situadas en el plano β. Por el punto Po, trazaremos una perpendicular al plano del cuadro п, punto P’, por donde trazamos una perpendicular a la charnela, traza βo del plano, obteniendo el punto c. Haciendo centro en c y radio ρ, describimos un arco que cortará a la perpendicular en el punto P’1. Los puntos A y B son puntos dobles, por tanto estarán abatidos en si mismo. La unión de A y B con P’1, nos darán las rectas r’ y s’ y con ellas el ángulo que forman. Hemos utilizado como charnela la traza βo del plano.
En el plano seguiremos el mismo procedimiento. Sean las rectas r’ y s’, que se cortan en el punto P’(3), y situadas en el plano cuya l.m.p. es la recta p’. Utilizaremos como charnela la traza βo del plano.
Los puntos A y B, dos puntos dobles por encontrase en la charnela.
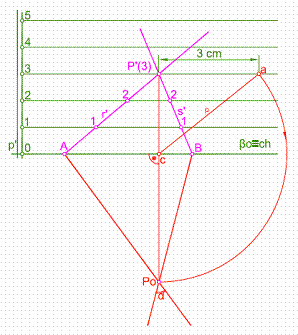
Figura 54
Par abatir el punto P’, trazamos una perpendicular a la charnela por dicho punto, cortando a esta en c.
Sobre la horizontal de plano de cota 3, llevamos 3 cm, punto a, que unimos con c. Haciendo centro en c y con radio de giro ρ, trazamos un arco hasta que corte a la perpendicular en Po. La unión de Po con A y B nos determina el ángulo.
1.2. Angulo que forma una recta con un plano.
Podemos observar en el espacio los pasos que se van a seguir. Se pide hallar el ángulo que forma la recta r con el plano п. Como puede comprobarse, el ángulo que forma la r recta con el plano п es el mismo que forma dicha recta con su proyección i.
Para resolver el problema seguiremos los pasos siguientes: Figura 55.
1) Tomaremos un punto cualquiera en la recta r, por ejemplo P’(6), y por el trazaremos una perpendicular al plano, hallando previamente el intervalo de la recta is.
2) A continuación haremos contener a la recta r’ y a s’, en un plano de l.m.p. n’.
3) Hallaremos la intersección del plano n’ con p’, recta i’., que cortará a s’ en el punto I’(0,113).
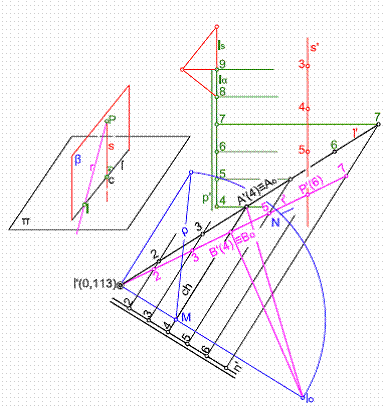
Figura 55
4) Abatiremos la recta i’ y la recta r’, tomando como charnela la horizontal de plano de cota 4. Los puntos A’ y B’, por estar en la charnela son puntos dobles estando abatidos en si mismo.
5) Sobre el punto I’, llevamos la diferencia de cotas entre la chanela y 4- 0,113= 3,88 cm. Con el radio de giro ρ, y haciendo centro en M, trazamos un arco que nos determina el punto Io, que unido con Ao y Bo, nos dará el ángulo buscado α.
1.3. Angulo que forman dos planos.
Para su resolución se pueden emplear dos métodos:
a) Trazar un plano perpendicular a la arista de intersección de ambos plano.
b) Trazar por un punto cualquiera rectas perpendiculares a los dos planos .
Primer procedimiento: Figura 56. Consideremos dos plano en el espacio α y β. Hallamos la recta r intersección de ambos. Seguidamente trazamos por un punto cualquiera por ejemplo P, un plano δ perpendicular a r, cortando a los planos α y β según t y v. Por abatimiento de estas rectas obtendremos el ángulo que forma con los planos.
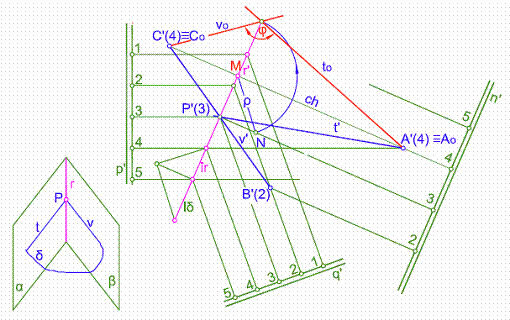
Figura 56
Resolvamos el problema en el plano.
1) Sean los planos α y β, dados por su l. m. p. p’ y q’, respectivamente.
2) Hallamos la intersección de ambos planos, recta r’.
3) Por un punto cualquiera de la recta r’ por ejemplo P’(3), trazamos un plano perpendicular a ella, previamente hallaremos el intervalo del plano iδ, plano de l. m. p. n’.
4) Seguidamente hallamos la intersección de este plano n’ con los planos q’ y p’, rectas t’ y v’.
5) Elegimos como charnela la horizontal de plano n’ de cota 4. Los puntos Ao y Co por estar en la charnela son puntos dobles y están abatidos en si mismo. El resto del ejercicio es similar al anterior.
Segundo procedimiento: Figura 57.
1) Elegimos un punto cualquiera del espacio, por ejemplo P’(3).
2) Por dicho punto trazamos dos rectas perpendiculares a ambos planos, t y v, hallando previamente los intervalos de ambas rectas.
3) Hacemos contener a las rectas t’ y v’ en un plano de l. m. p. n’.
4) Utilizando como charnela la horizontal de plano de cota 4, abatimos las rectas, obteniendo to y vo.
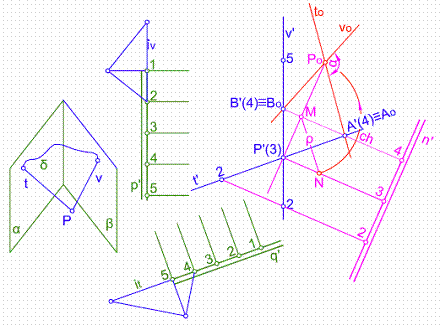
Figura 57


