- 1. Abatimientos
Los abatimientos son utilizados en la geometría descriptiva para obtener verdaderas magnitudes. Trabajaremos primero en el espacio.
Decimos que abatimos un plano sobre otro, cuando hacemos superponer el primero sobre el segundo, haciendo girar alrededor de un eje, llamado charnela, que es la intersección de ambos. Con los abatimientos se pretende obtener verdaderas magnitudes de rectas o figuras planas.
En este capítulo se habrá de abatir puntos y rectas, pero realmente los que haremos será abatir el plano que las contiene
1.1. Mecanismo de los abatimientos.
Adoptaremos un punto P, situado en el plano α , abatimos dicho plano α que contiene al punto P, utilizando como charnela ch la intersección de los planos α y δ. Figura 45.
La mínima distancia del punto a la charnela MP, será el radio de giro ρ, el cual se halla como hipotenusa del triángulo rectángulo cuyos catetos son P’ M ( distancia del punto a la charnela) y P’ (P) ( cota del punto con respecto al plano de abatimiento).

Figura 45
En lugar de operar en el espacio lo haremos sobre el plano de proyección. Abatimos el triángulo MPP’, sobre el plano de proyección MP(P). La circunferencia de centro M y radio M(P) = ρ cortará a la perpendicular a la charnela en los puntos (P)o y (P’)o, puntos abatidos.
Como puede observarse en la figura, en el triángulo MP’(P), se cumple que:
a) Que el radio de giro ρ, se ha hallado trazando una perpendicular a la charnela ab.
b) Que P’M es perpendicular a la charnela ch, en el punto M.
c) Que P’(P), es paralela a la charnela, y cuya magnitud es la cota del punto con respecto al plano de abatimiento y coincide con la horizontal de plano de la misma cota.
Ahora trabajaremos en el sistema de planos acotados. Figura 46. Consideremos un plano α dado por su l.m.p. graduada n’. Utilizaremos como charnela la traza del plano αo. Por un punto cualquiera, por ejemplo P’(1) se traza la perpendicular a la charnela y una paralela que en este caso coincide con la horizontal de plano 1. Sobre la paralela se toma un segmento igual a la cota P’(1) N. El radio de ρ giro será la distancia de MN. Con centro en N trazamos un arco que cortará a la perpendicular a la charnela en los puntos Po y P’o.
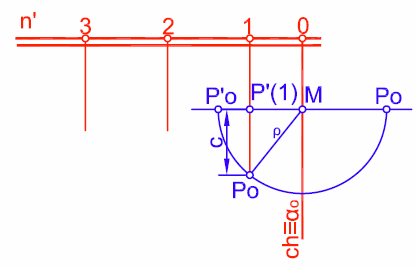
Figura 46
1.2. Abatimiento de un plano
Un plano cualquiera se puede abatir sobre un plano horizontal cualquiera, solo hay que tener encuentra que sobre la recta paralela a la charnela debemos de tomar la diferencia de cotas entre el punto y el plano que pase por la charnela. Figura 47.
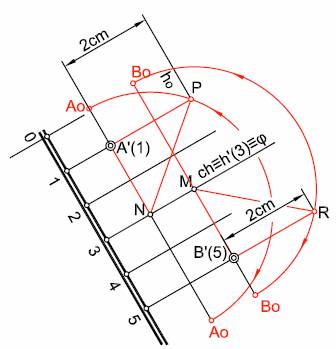
Figura 47
En la figura se ha tomado como plano de abatimiento el horizontal de cota h’(3). Si tomamos el punto A’(1), trazamos una perpendicular a la charnela y sobre la horizontal de plano h’(1), llevamos la diferencia de cotas con la charnela es decir 2 cm. Haciendo centro en N, trazamos un arco que corte a la perpendicular a la charnela en el punto Ao, que será el punto abatido del plano. Lo mismo repetiremos con el punto B’(5). Como puede apreciarse para abatir el plano lo que hemos realizado es el abatimiento de la figura o punto contenido en el plano.
1.3. Abatimiento de una recta
Para abatir una recta, bastará con abatir dos puntos de la misma.
Sea el plano dado por su l.m.p. n’, una recta r’ contenida en el mismo.
Elegimos un punto cualquiera de la recta, por ejemplo el punto P’(10) y lo abatimos utilizando con charnela la horizontal de plano de cota 8. Figura 48.
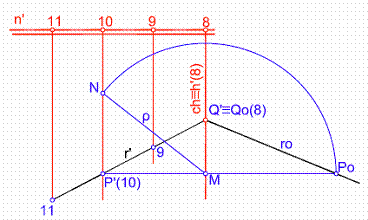
Figura 48
Por el punto P’(10) trazamos una perpendicular a la charnela P’ M y una paralela que coincide con la horizontal de plano de cota 10. Llevamos a partir de P’ la diferencia de cotas 10-8 = 2 cm. Trazamos un arco de radio de giro ρ =MN. Este cortará a la perpendicular P’M en Po, punto abatido. El punto Q se obtiene de forma directa ya que por estar en la charnela es un punto doble y su abatimiento coincidirá con el punto. La unión de ambos puntos nos da la recta abatida ro.
1.4. Abatimiento de una figura plana
Entre la proyección de una figura plana contenida en un plano α, la proyección ortogonal sobre el plano del cuadro y la figura abatida sobre dicho plano existe una relación de afinidad en la que se cumple que:
d) Eje de afinidad Ea: Será la traza del plano o charnela.
e) Dirección de afinidad Da: Rectas perpendiculares a la charnela
f) Dos rectas afines se cortan en el mismo punto del eje de afinidad.
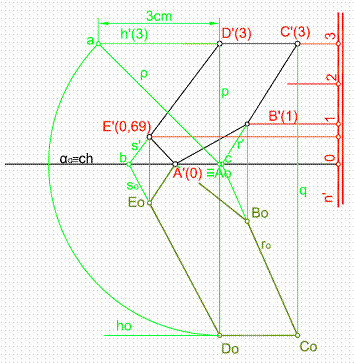
Figura 49
Sea la figura plana dada por los puntos en proyección A’, B’, C’, D’, E’, situada en un plano α dado por su l.m.p. n’. Figura 49.
1) El primer paso será abatir el punto D’. Para ello trazaremos por D’ una perpendicular a la charnela ch y sobre la horizontal de plano 3 y a partir de D’ llevaremos tres unidades. Con centro en c y radio de giro ρ, trazamos un arco hasta que corte a la perpendicular p, obteniendo el punto Do.
2) Seguidamente prolongaremos la recta s, obteniendo el punto b y por afinidad obtenemos Do.
Continuando con restas afines hallamos el resto de los puntos.
1.5. Elevación de una figura plana
Este ejercicio es inverso al anterior. Partiremos de una figura en verdadera magnitud y hallaremos su proyección sobre una plano en el que se conoce un vértice de la figura y su traza αo.
Sea la figura Ao, Bo, Co, Do, dada en verdadera magnitud situada en el plano cuya traza es αo, que se conoce, así como el punto B’ de cota 2. Se pide hallar la proyección de dicha figura 50.
1) El primer paso será hallar el plano que contiene a la figura.
2) Para ello trazamos por Bo una perpendicular c a la charnela, llevando, a continuación sobre ella 2 cm.
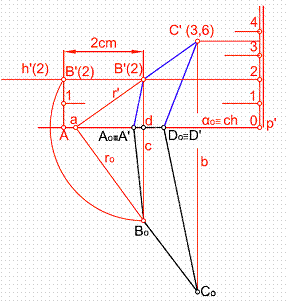
Figura 50
3) Haciendo centro en el punto d intersección de la perpendicular con la charnela, trazamos un arco que corte a la recta AB’ en el punto de cota 2, horizontal del plano que buscamos.
2) Los puntos Ao y Do, por estar en la charnela son puntos dobles.
3) Prolongando la recta ro hasta que corte a la charnela punto a. La recta r’ será afín de ro y nos determinará el punto C
1.6. Proyecciones de una circunferencia.
Dado un plano por su l.m.p. graduada, situar una circunferencia de diámetro 25 mm., cuyo centro tiene de cota 3,5 cm. Figura 51.
1) Trazamos la horizontal de plano de cota 3,5 cm.
2) En un punto cualquiera de ella situamos el centro O’(3,5)
3) Por el punto 0 de la l.m.p. trazamos αo que será la charnela ch.
4) A partir de O’ llevamos 3,5 cm, uniendo el punto a con c.
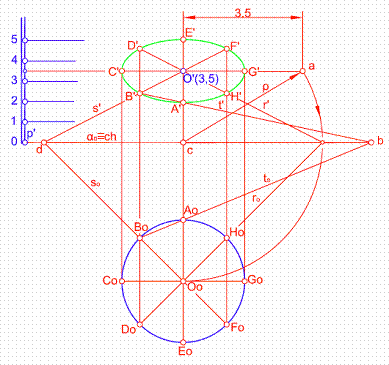
Figura 50
5) Con el radio de giro ρ trazamos un arco que corte a la perpendicular a la charnela por O’ en el punto Oo, centro de la circunferencia de diámetro 25 mm.
6) Dividimos la circunferencia en un número de partes, por ejemplo 8.
7)Trazamos la recta so y su afín r’, obteniendo sobre la perpendicular a la charnela que pasa por DoBo, los puntos B’D’.
8)El resto de los puntos de obtienen de forma análoga.
1.7. Ejercicio. Resolución de una cubierta y abatimiento de una de sus vertientes.
Sea la cubierta dada por los puntos D, E, F, G, H, que tiene un patio de luces I, J, K, L. El intervalo para todas sus vertientes será 0,5 cm. Se pide.
A) Resolver la cubierta.
B) Hallar la superficie del alero A’, B’, C’, E, D.
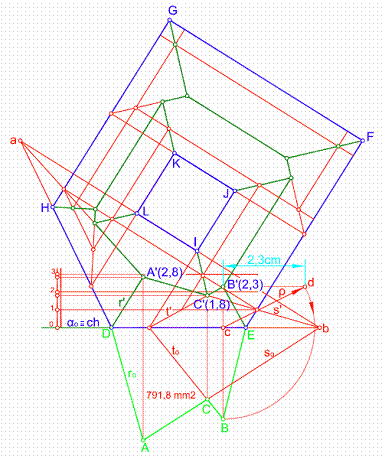
Figura 52
1) Trazamos todas las horizontales de plano con intervalo 0,5 cm. Figura 52.
Las intersecciones de los planos que concurren en los vértices de la cubierta se hallan trazando las bisectrices de sus ángulos, o bien uniendo las horizontal de cota 0 y la de cota 1.
2) Seguidamente hallamos la intersección del plano de traza HD con el plano de traza JK.
El resto de las intersecciones son semejantes.
3) Para hallar la verdadera magnitud del alero A’, B’,C’, E, D, trazamos la línea de máxima pendiente de este plano y la graduamos, obteniendo las cotas de los vértices A’(2,8), B’(2,3) y C’(1,8).
4) Seguidamente por un punto cualquiera, por ejemplo el B’(2,3), trazamos un perpendicular a la charnela que cortará a esta en el punto c. Llevamos 2,3 cm. sobre la horizontal de plano a B’. Haciendo centro en c con el radio de giro ρ, trazamos un arco que corte a la perpendicular cB’, en el punto B. El resto del ejercicio se resuelve por afinidad.
Para hallar la superficie, bastará con resolver un pequeño ejercicio de geometría.


