- 1. Ejercicios de aplicación
La utilización practica de las intersecciones de planos es la resolución de las cubiertas de un edificio, partiendo del plano de la última planta del mismo. Deberemos de conocer la pendiente de cada uno de los planos inclinados. Su resolución se realizara hallando la intersección de todos los planos que se formen con los lados del polígono.
1.1. Dada la poligonal de aleros de la figura y las pendientes indicadas, para cada uno de los faldones. Dibujar las proyecciones de la cubierta, siendo el tejado de la zona ABCD a dos aguas.
1) Partimos de la poligonal A, B, C, D, E, F, G, H. Teniendo en cuenta que la pendiente P = 1/i, Los aleros con pendiente 1, trazaremos las horizontales de plano a 1 cm. Los aleros con pendiente 2, las horizontales de plano estarán a 0,5 cm. Figura 42.
2) Una vez trazadas las l.m.p. y las horizontales de plano, pasaremos a trazar las rectas intersección de los distintos planos. La zona ABCD, que es a dos aguas las l.m.p. son paralelas, para hallar la intersección, utilizaremos unos de los métodos visto anteriormente
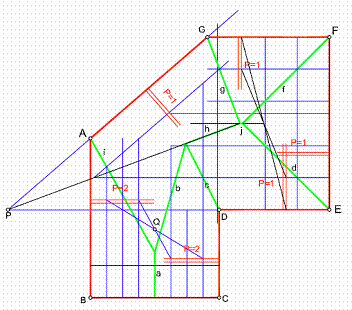
Figura 42
3) Uniremos la horizontal 1 del plano CD con la 1 del plano BC y la 2 del plano CD con la 2 del plano AB. La arista a debe pasar por el punto Q de intersección de ambas rectas y ser paralelo al alero.
La zona DFGH, tendrá varias intersecciones.
4) Comenzaremos por los faldones DE y EG. Al tener la misma pendiente, su intersección será la bisectriz del ángulo formado por ambas rectas. También se puede hallar uniendo el punto de intersección de las horizontales de valor 1 y las de valor 2. De esta forma obtendríamos la recta d y f.
5) Seguidamente debemos comprobar si existen otras intersecciones. Unimos la horizontal de valor 0 del plano DE con la 0 del plano AG, que nos determina la recta h. Por el mismo procedimiento hallamos el resto de las intersecciones.
1.2. Dada la cubierta de un edificio de forma pentagonal con un patio de luces interiores. Representar la cubierta del tejado, teniendo en cuenta que las pendientes exteriores tienen 2/3 y las del patio de luces de ½. Figura 43.
1) El primer paso será calcular los intervalos de la cubierta que serán el inverso de la pendiente.
Pendientes exteriores 3/2 = 1.5 cm.
Pendientes interiores 2/1 = 2 cm.
2) Seguidamente trazamos las líneas de máxima pendiente y con el calculo anterior las horizontales de plano.
3) Pasamos a continuación a hallar las intersecciones de los distintos plano.
4) Las intersecciones de los planos A, B, C , D, F, serán las bisectrices de los ángulos, o bien la unión de las horizontales de plano de cota 0 y las de cota 1. Recta Qbc.
5) Seguidamente hallamos la intersección de los plano paralelos AF y GJ, determinando el punto P. La intersección será paralela a las horizontales de plano. Determinando los puntos a y j.
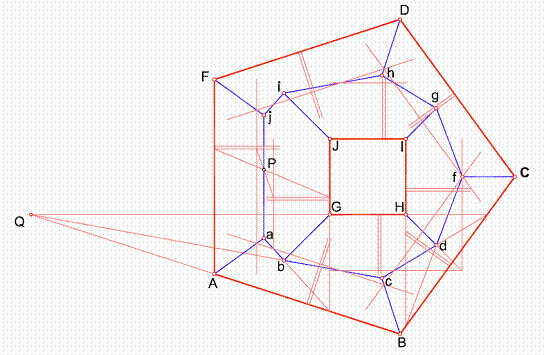
Figura 43
El resto de los puntos se hallan de forma similar a lo anteriores.
1.3. Construir la cubierta del tejado cuya planta es la de la figura, teniendo presente que todos los intervalos valen 0,5 cm. Figura 44.
1) El primer paso será dibujar las líneas de máxima pendiente que sean necesarias, trazando posteriormente las horizontales de plano.
El resto del ejercicio es similar al visto con anterioridad.
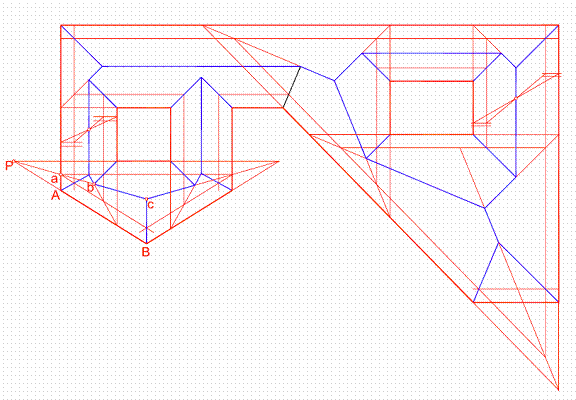
Figura 44


