1.1. Rectas perpendiculares.
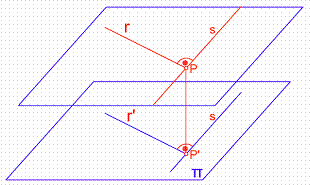
Figura 30
El teorema de las tres perpendiculares dice: Si dos rectas r y s son perpendiculares entre si y una de ellas s es paralela al plano de proyección, sus proyecciones ortogonales serán perpendiculares. Figura 30.
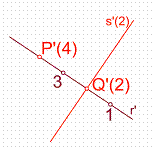
Ejercicio: Trazar por el punto P’(4), una recta perpendicular a la s’(2).
Bastará con trazar por el punto P’(4) una recta perpendicular a s’(2). El punto de corte Q’ tendrá de cota 2. Finalizamos graduando el resto de la recta. Figura 31.
1.2. Recta perpendicular a un plano.
Una recta r es perpendicular a un plano, α cuando lo es a una recta s cualquiera contenida en dicho plano. Figura 32.
Para que la recta sea perpendicular al plano ha de cumplirse que:
a) La proyección de la recta ha de ser perpendicular a la traza del plano
b) Las pendientes han de ser inversas, ir x iα = 1.
c) Deben de estar graduadas en sentido opuesto.
Ejercicio: Trazar por el punto A’(6), una recta que sea perpendicular al plano α.
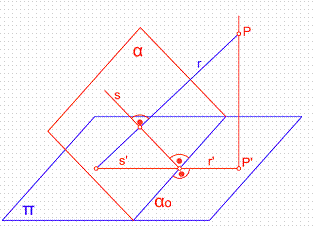
Figura 32
El primer paso será hallar el intervalo de la recta. Para ello, levantamos por un punto cualquiera P, una perpendicular a la l.m.p. del plano α, llevando sobre ella 1 cm. punto P’. La recta P’4, por dará la inclinación del plano α. Trazamos una perpendicular a la recta anterior, obteniendo el punto a. La distancia Pa, será en intervalo ir de la recta que buscamos. Figura 33.
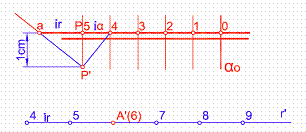
Figura 33
Trazamos por el punto A’(6) una paralela a la l.m.p. del plano α y con el intervalo calculado ir, graduamos la recta en sentido inverso.
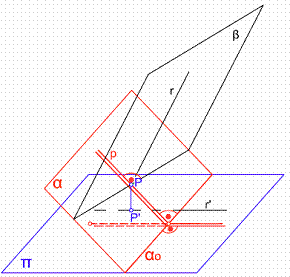
Figura 34
1.3. Perpendicularidad entre planos
Para que dos planos α y β sean perpendiculares, bastará con uno de ellos por ejemplo el β contenga una recta r que sea perpendicular al plano α. Figura 34
Ejemplo: trazar por el punto P una plano perpendicular al plano α. Este ejercicio tendrá infinitas soluciones, ya que por un punto pueden pasar infinitos planos perpendiculares.
Trazaremos por el punto P una recta perpendicular al plano α, ejercicio visto anteriormente). Cualquier plano que pase por este punto cumplirá con lo pedido. Figura 35.
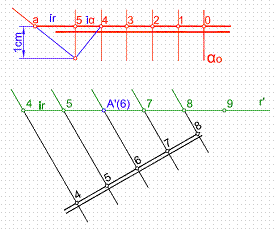
Figura 35
- 2. Distancia entre dos puntos.
Sean los puntos A(1) y B(2), en el espacio y proyectemos estos puntos sobre el plano del cuadro obteniendo A’ (1) y B’(2), la distancia d, será la proyección sobre el cuadro del segmento AB = d. Figura 36.
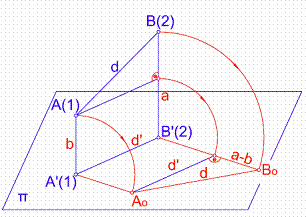
Figura 36
Si por el punto A(1) trazamos una paralela al cuadro obtendremos d’. La distancia a B(2) será la diferencia de cotas de los puntos A y B. De ello se deduce que las distancia entre dos puntos cualquiera del espacio A y B, será la hipotenusa del triángulo rectángulo formado por la proyección de la recta sobre el cuadro d’ y la diferencia de cotas a.
En el plano, operaríamos de ña forma siguiente: trazamos por los puntos A’(1) y B’(2), dos perpendiculares a la recta que une ambos puntos r’, llevando sobre ellas 1 y 2 cm respectivamente, obteniendo los puntos Ao y Bo. La hipotenusa d del triángulo formado por d’ y la diferencia de cotas a-b, será la distancia en verdadera magnitud entre los puntos A y B. Figura 37.
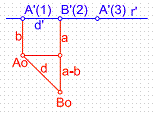
Figura 37
2.1. Distancia de un punto a una recta
Veremos un esquema en el espacio, al igual que ya se hizo con el sistema diédrico. Figura 38.
Sea el punto A contenido en el plano α y la recta r, trazamos por A un plano perpendicular α a la recta r, seguidamente hacemos contener a dicha recta en un plano cualquiera β. Hallamos la intersección de los planos α y β, dicha intersección nos determina el punto I. La distancia que separa el punto A de la resta r será la recta AI.
Trabajando en el plano, tendremos el punto A’ (5) y una recta r’ graduada. Por dicho punto, trazaremos un plano p’ perpendicular a la recta r. Hallando previamente el intervalo del plano iα, como se ha visto con anterioridad.
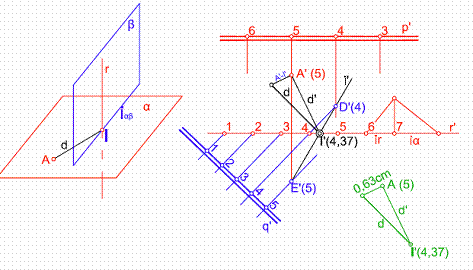
Figura 38
Seguidamente hacemos pasar por la recta r’ un plano cualquiera de l.m.p q’, hallando a continuación la intersección de ambos planos recta i’, Esta corta a la recta r’ en el punto I’(4,37). La unión de I’ y A’, nos dará la distancia entre el punto y el plano.
Para hallar la verdadera magnitud de d’. levantaremos por A’ (5) una perpendicular a d’ y llevando sobre ella la diferencia cotas 5-4,37 = 0,63cm, La distancia en verdadera magnitud, será la hipotenusa del triángulo rectángulo formado.
2.2. Distancia de un punto a un plano
Realizaremos el ejercicio en el espacio. Por el punto A trazamos una recta perpendicular al plano α. Hacemos contener a la recta en un plano cualquiera β. Hallamos la intersección del plano α y β, recta i α β, que cortara a r en el punto I. La distancia AI, será la que buscamos.
Trabajemos ahora en el plano.
Sea el punto A’(6) y el plano dado por su l.m.p. p’. Por el punto A, trazamos una recta r’ paralela a p’,hallando previamente el intervalo de la recta ir. Con el intervalo hallado graduamos en sentido contrario. Figura 39.
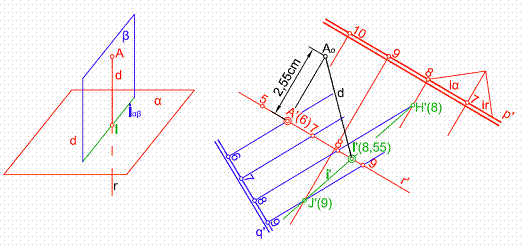
Figura 39
Seguidamente hacemos contener a la recta r en un plano cualquiera q’, hallando, a continuación la intersección i’ de ambos planos, dicha intersección cortará a r en el punto I’(8,55). La distancia en proyección será la recta A’(6)-I’(8,55)
Para hallar la verdadera magnitud levantamos por A’(6) y recta una perpendicular y llevamos sobre ella la diferencia de cotas 8,88-6 = 2,55. La unión de Ao con I’ será la verdadera magnitud de la distancia d que separa el punto A del plano α,
2.3. Distancia entre dos planos paralelos
Sean los planos paralelos α y β. Elegimos un punto cualquiera P del plano β, trazamos por el una recta r perpendicular a ambos planos. Seguidamente hacemos pasar por la recta r un plano cualquiera δ, hallando a continuación la intersección con el plano α, recta iαβ,
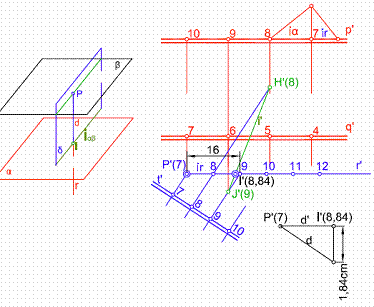
Figura 40
obteniendo en la recta r, el punto I, La distancia PI, será la que separa el punto del plano.
Para trabajar en el plano seguiremos los mismos pasos.
Sean los planos paralelos α y β, cuyas l.m.p. son p’ y q’. Elegimos en el plano β el punto P’(7), trazando por el una recta perpendicular, calculando previamente el intervalo de la recta ir. Figura 40.
Hacemos contener a la recta r en un plano cualquiera por ejemplo el plano δ, de l.m.p. t’.
Hallamos la intersección con el plano de l.m.p. p’. La recta J’H’ cortará a r’ en el punto I’(8,84). La distancia en proyección será la recta P’(7)- I’(8,84)
Para hallar la verdadera magnitud, construimos un triángulo rectángulo en el que un cateto sea la distancia P’I’ y otro cateto la diferencias de cotas 1,84 cm. Su hipotenusa d será la distancia buscada.
2.4. Distancia entre dos rectas paralelas.
Sean las rectas r y s en el espacio, elegimos un punto cualquiera J de la recta s y trazamos un plano α perpendicular a ambas rectas. Hacemos pasar por r un plano cualquiera β, hallando su intersección con el plano α. La distancia JI, será la buscada.
En el plano operamos de la misma forma. Sean las rectas graduadas r’ y s’. Por un punto cualquiera de la recta s’, por ejemplo J’(4),
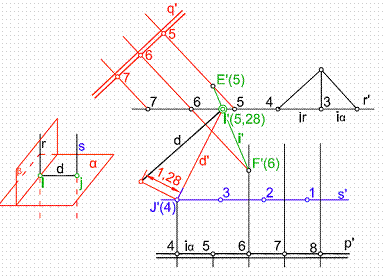
Figura 41
trazamos un plano α de l.m.p. p’. Previamente hallaremos el intervalo del plano iα.
Seguidamente hacemos contener a la recta r’ en un plano l.m.p. q’.
Hallamos la intersección del plano p’ y q’, recta i’. Esta recta corta ala r’ en el punto I’ (5,28).
El resto es similar al ejercicio anterior. Figura 40.


