- 1. Intersección de planos
1.1. Intersección de dos planos oblicuos cualquiera.
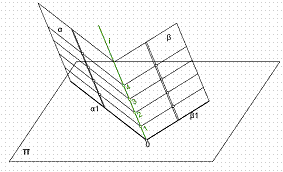
Figura 24
La intersección de dos planos α y β es una recta i , definida por dos puntos. Esta recta puede ser propia o impropia en el caso de que los planos sean paralelos entre si.
Consideremos en el espacio dos planos oblicuos α y β, dados por su línea de máxima pendiente, r’ y s’. Figura 24. La intersección del plano α con el plano del cuadro п será la traza α1. La intersección del plano β con el plano п será la traza β1. El punto 0, pertenecerá a los tres planos y por tanto será un punto de la intersección que se busca. Otro punto cualquiera se halla trazando dos horizontales de plano cualquiera.
Si los planos tienen la misma pendiente, el intervalo será el mismo. En este caso la intersección de los plano será la bisectriz del ángulo formado por las trazas del plano.
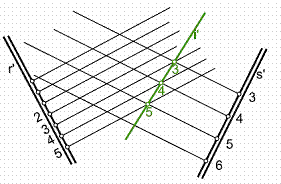
Figura 25
Para hallar la intersección en el plano, bastará con unir los puntos de intersección de dos de las horizontales de planos de la misma cota. En la Figura 25 será la recta i’ que une los puntos de cota 5 y 3.
1.2. Intersección de dos planos cuyas trazas son paralelas. Planos paralelos.
La línea de máxima pendiente será paralela en proyección. En la figura 26, tenemos los planos α y β en el espacio. Al abatirlos sobre el cuadro las l.m.p. q’ y p’ quedaran paralelas, su intersección también será paralela a las horizontales de plano. Por lo tanto conociendo un solo punto es suficiente para obtener la intersección de dos planos.
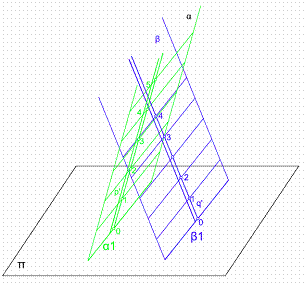
Figura26
Para obtener el punto de intersección en el plano, basta con unir dos parejas de puntos homólogos, (igual cota). Por el punto de intersección de ambas rectas pasara la intersección de los planos P’ (2,71). Punto que como puede observarse pertenece a ambos planos. Figura 27.
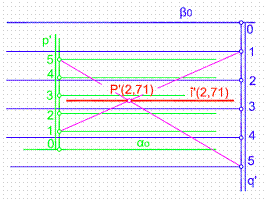
Figura 27
Este ejercicio se puede resolver, por medio del abatimiento de los planos.
Se cortan ambos planos por otro γo perpendicular a las trazas. Seguidamente abatimos ambos planos Q’Po y T’Po. Hallamos los ángulos que forman con el cuadro α y β, el punto de intersección de las l.m.p. abatidas Po, nos dará la cota de la intersección, 2,71 cm. Figura 28.
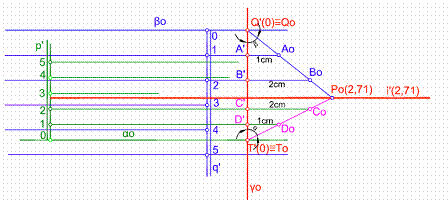
Figura 28
Los planos pueden formar, aristas o goteras. Cuando forman arista, la graduación de la l.m.p, aumenta. Si forma gotera, disminuye. Figura 29.
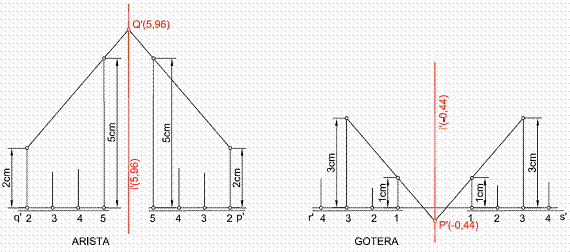
Figura 29
“Ir al ïndice”


