- 1. Alfabeto del Plano
1.1. Plano oblicuo cualquiera.
Se denomina traza de un plano α a la intersección de este con el plano del proyección i п ho.
Recta horizontal de plano será aquella que es paralela al plano del cuadro, h1, h2, h3, …
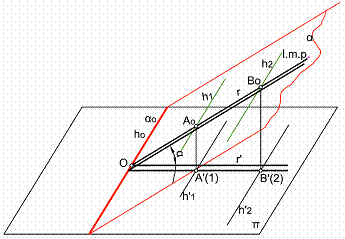
Figura8
Se llama línea de máxima pendiente, que la representaremos por ( l.m.p.) de un plano, al igual que en el sistema diédrico, a aquella que es perpendicular a la traza del plano.
Como puede apreciarse en la figura en la figura 8, hemos considerado un plano en el espacio α, la intersección de dicho plano con el de proyección п vendrá dada por la recta ho. La recta perpendicular a esta traza, será la línea de máxima pendiente l.m.p.
Consideremos en el plano α, dos puntos cualquiera de cota entera, por ejemplo Ao y Bo, tranzamos por dichos puntos dos horizontales de plano, h1 y h2. Seguidamente proyectemos todo el conjunto sobre el plano del cuadro, obteniendo los puntos A’(1) y B’ (2), Las horizontales de plano h’1 y h’2, serán paralelas a la traza αo y pasarán por dichos puntos. La l.m.p. r’ se obtendrá uniendo los puntos A’ y B’ y será perpendicular a la traza del plano.
En la figura 9 puede apreciarse la representación de un plano en proyección con la l.m.p. graduada.
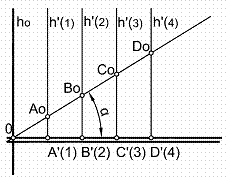
Para obtener el ángulo que forma un plano cualquiera con el plano de proyección, llevaríamos sobre unas perpendiculares la l.m.p, en los puntos A’(1) 1 cm y C’(3) 3 cm., obteniendo dichos puntos en verdadera proyección Ao y Co, que unidos, cortará a ho en el punto O, obteniendo el ángulo α. Figura 9.
De todo los anterior se deduce que un plano queda definido por:
a) Por tres puntos no alineados.
b) Por su recta de máxima pendiente graduada.
c) Por dos horizontales de plano cualquiera acotadas.
En este segundo caso bastará con trazar una perpendicular a dichas rectas para obtener su l.m.p.
1.2. Plano paralelo al de proyección o plano horizontal.
Se representa por:
a) Tres puntos de igual cota
b) Dos rectas horizontales que se corten.
c) Dos rectas paralelas.
Este plano por ser horizontal, no tendrá traza y su cota será la misma en cualquier punto del plano. Figura 10.
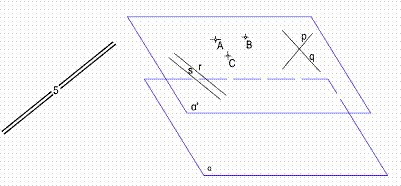
Figura 10
1.3. Plano Perpendicular al de proyección, plano vertical.
Este plano se llama también plano proyectante, viene reprensado por su traza αo, Su l.m.p. es una recta de punta A’ (5). Su intervalo será 0. Figura 11.
- 2. Pertenencias
Un punto pertenece a una recta si su cota coincide con la de la recta y su proyección está sobre ella. El punto D’ (4), pertenece a la recta. El punto B’ (5), ( figura 12) no pertenece a la recta, ya que su numeración no coincide con la recta, aunque su proyección esté sobre ella. Dicho punto estará encima de la recta.
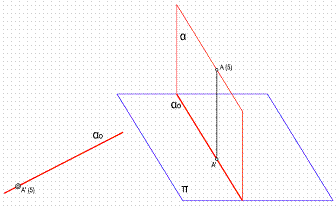
Figura 11
Un punto estará contenido en un plano cuando pertenezca a una recta cualquiera del plano. Sea un plano dado por su línea de máxima pendiente graduada. Figura 13. Tracemos por los puntos 1, 2….horizontales de plano. El punto A’ (1) pertenecerá al plano ya que se encuentra sobre una horizontal de la misma cota. El punto Q’ ( 5) , está por encima del plano.
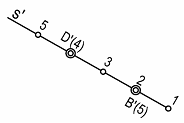
Figura 12
Para situar una recta sobre un plano bastará con que los puntos de la recta estén sobre las rectas horizontales homónimas del plano. Figura 14.
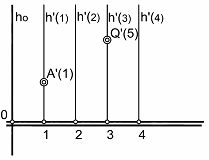
Figura 13
Ejemplo: Definir un plano dado por los puntos C’(3), H’ (5) y G’(7). Figura 15.
Unimos dos puntos cualquiera, por ejemplo el C’(3) y G’(7). Ahora tendremos un punto y una recta r’. Graduamos la recta r’y unimos el punto C’(3) con el H’(5) obteniendo la recta s’, que graduamos. Unimos los puntos de la misma cota de ambas rectas obteniendo las horizontales de plano. Una perpendicular a ellas nos dará la l.m.p. del plano buscado.
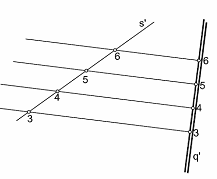
Figura 14
- 3. Ejercicios Resueltos.
3.1. Dado un punto B’ (4) de la recta s’ cuya pendiente es de 0,5, situar en la misma un punto cuya cota sea de 2. Figura 16.
Teniendo en cuenta que la pendiente P = 1/i = 1/0,5 = 2 cm.
Graduamos la recta s’ a partir de punto 4, en cualquiera de los sentidos la recta en partes iguales de 2 cm.
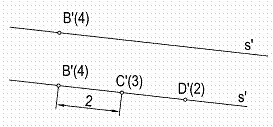
Figura 16
3.2. Dada la recta r’ por dos pares de puntos B’(2) y D’(4), graduarla y hallar la traza de la misma y el ángulo que forma con el plano del cuadro. Figura 17.
Levantamos dos perpendiculares a la recta r’ en los puntos B’ y D’, y sobre ella llevamos 2 cm y 4 cm respectivamente. Unimos los puntos Bo y Do por una recta que cortará a la r’ en el punto T’(0), traza de la recta con el plano del cuadro.
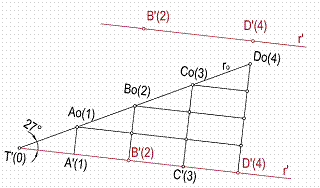
Figura 17
3.3. Dada la recta r’ por los puntos A’(1,3) y B’(-0,5), graduarla y hallar la traza de la misma. Figura 18.
Levantamos por los puntos A’ y B’ dos rectas perpendiculares y llevamos sobre ellas, 1,3 cm. en un sentido y el en otro 0,5 cm, obteniendo los puntos Ao y Bo, que unidos obtenemos la recta ro en verdadera posición. La traza de la recta será el punto de intersección de ro con r’. Trazamos una paralela a la recta r’ con el valor de 1 cm, obteniendo el punto 1. El intervalo de la recta será T1.
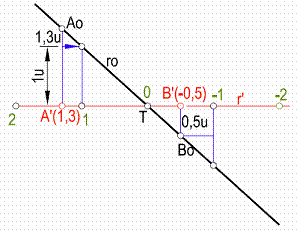
Figura 18
3.4. Dado un plano por tres puntos no alineados, determinar sus elementos: Traza, Línea de máxima pendiente y su Graduación. Figura 19.
Sean los puntos A’(1), B’(2) y D’(4). Unimos los tres puntos por tres rectas, triángulo A’B’D’. Graduamos dos de ellas, obteniendo los puntos 0 y 0’, traza de las rectas. Uniendo los dos puntos tendremos la traza del plano αo y la dirección de las horizontales de plano.
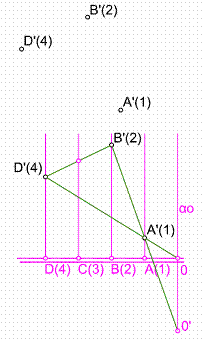
Figura 19


