1. FUNDAMENTOS DE LA PERSPECTIVA AXONOMÉTRICA.
Cuando dibujamos lo hacemos sobre un medio de dos dimensiones, y pretendemos representar un objeto tridimensional. Por este motivo surgieron los medios de representación, entre los que se encuentra el sistema axonométrico, que estudiaremos a continuación
En el sistema diédrico pudimos observar que para definir una pieza, era necesario una, o más vistas de la misma. Esto nos obligaba a que el interprete tuviera una preparación adecuada del sistema. Sin embargo, en el sistema de perspectiva axonométrica, en una sola vista el cuerpo queda completamente definido, logrando una sensación de corporeidad no conseguida con el sistema diédrico.
Esto hace que este método sea un medio de comunicación sea e más adecuado entre el técnico y el profano. El único inconveniente es su laboriosidad.
>1.2. ELEMENTOS QUE INTERVIENEN EN EL SISTEMA
Imaginemos la esquina de la clase y que esta la apoyamos en la pizarra por el vértice O, (figura 1),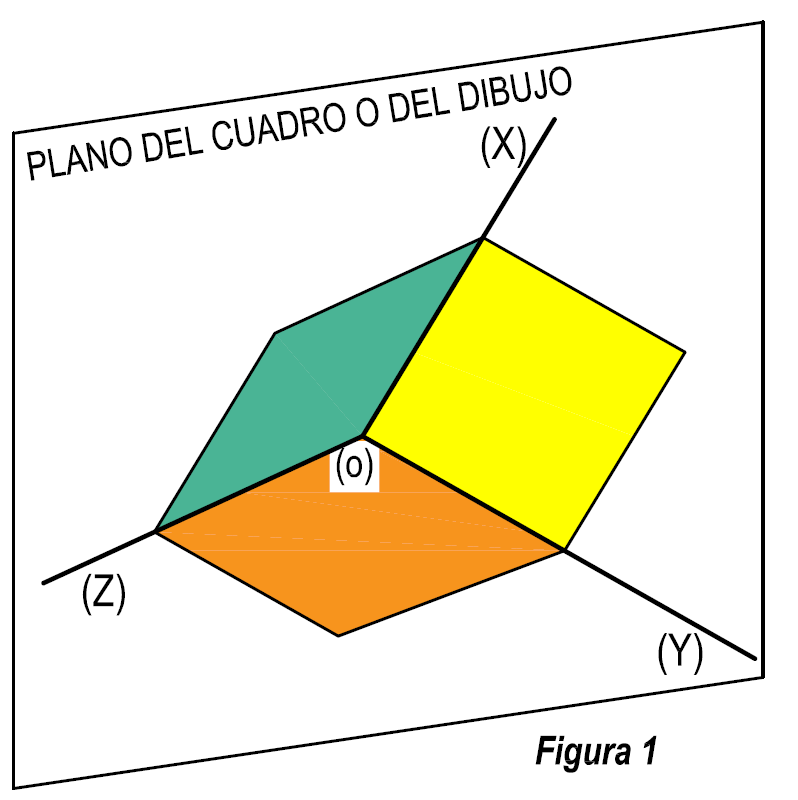
de tal forma que las aristas donde concurre el suelo y las dos paredes, quedan situadas en posición oblicua a la pizarra. La pizarra puede ser el plano del dibujo, llamada también plano del cuadro o plano proyectante.
El suelo y las dos paredes serán los planos proyectantes. Por tanto cuatro serán los planos que intervienen en el sistema, tres planos formado un triedro trirrectángulo y un cuarto plano que es el plano del dibujo. La única condición que deben cumplir estos planos es, que el plano del dibujo o cuadro no puede ser paralelo a ninguna cara o estar contenida en la misma.
La intersección de dos caras forman una arista, a la que llamaremos ejes coordenados, y por tanto serán tres los ejes.
La recta intersección de lo planos verticales ( las paredes) con el suelo, nos determinará el eje X e Y, y la intersección de las dos paredes el eje Z. El punto donde concurren los tres ejes le llamaremos vértice y lo designaremos por (O).
Estos tres planos forman un triedro trirrectángulo, y cada una de las aristas es perpendicular a la cara que no la contiene.
Una vez definidos los elementos que intervienen, vamos a indicar el mecanismo de proyección.
Situemos un punto en el centro de la clase, nos imaginamos una línea que pasando por dicho punto sea perpendicular al suelo y paredes de la clase. El punto de intersección de dicha línea con los planos ( suelo, y paredes), tendremos tres proyecciones. Figura 2.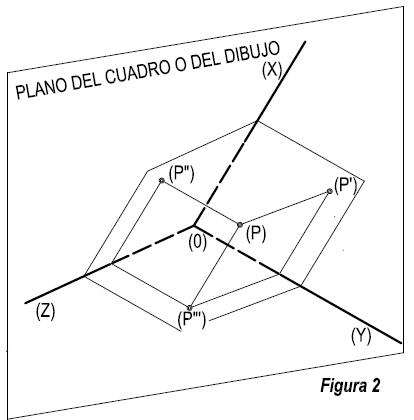 
De esta forma tendremos que, la proyección sobre el suelo la llamaremos horizontal, la situada en la pared derecha, vertical primera y la situada en la pared izquierda vertical segunda.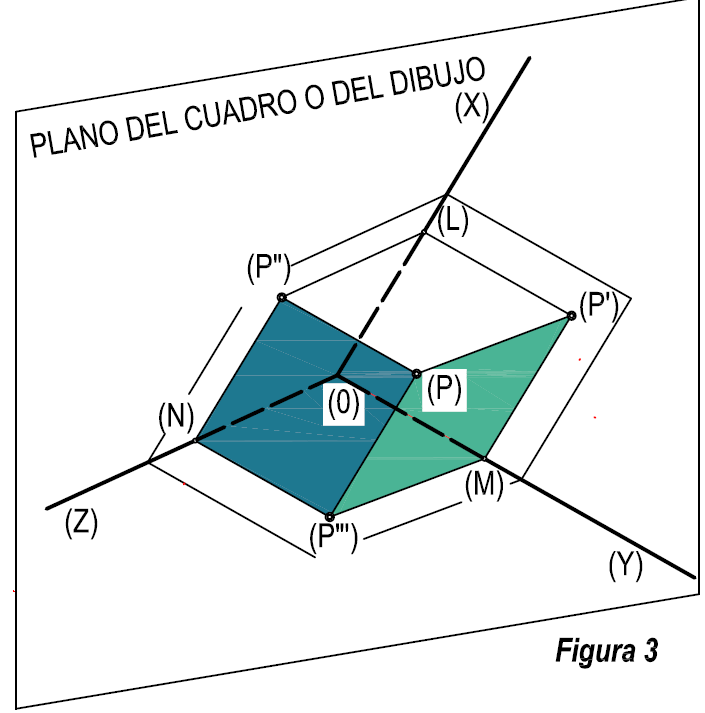
Ahora tendremos que establecer unos convenios que sean admitidos internacionalmente y que nos permitan interpretar una proyección. Por tanto un punto en el espacio será representado por una letra mayúscula encerrada entre paréntesis, y que sus proyecciones se representarán por la misma letra acompañada de una, dos o tres comillas, según sea la proyección, horizontal, vertical primera o vertical segunda respectivamente. Entendiendo que estas proyecciones se encuentran situadas en el espacio. (Figura 2).
Partimos de un punto en el espacio (P). (Figura 3 y 4). El primer paso es, proyectar sobre el plano del cuadro los ejes (X), (Y), (Z), (aristas del cubo formado por las paredes de la clase), de tal forma que el punto (L), se proyecte en L, el (M), en M, y el (N) en N. El punto (O), vértice del triedro que se encuentra apoyado en el plano del cuadro, se proyectará sobre si mismo en O. Uniendo el punto O con los puntos anteriores, tendremos los ejes en proyección X, Y, Z. (Figura 4).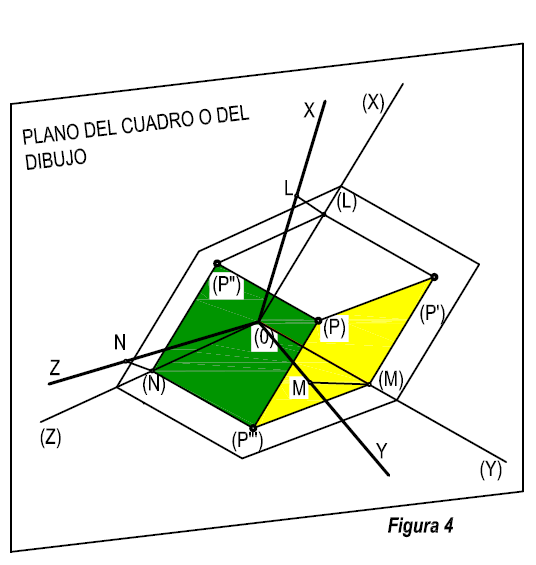
Tendremos que considerar que al proyectar sobre el cubo que forman las paredes de la clase, las proyecciones del punto ( P ), ( P’), ( P”) y ( P”’) , se encuentran en el espacio, y por tanto, en tres dimensiones.
Seguidamente pasamos a proyectar todo el conjunto sobre el plano del cuadro, de forma perpendicular, así tendremos que los puntos anteriores, se proyectan en P, P’, P ”y P”’. (Figura 5).
De acuerdo con lo anterior, un punto tendrá cuatro proyecciones, una proyección directa P, que es la que se entiende por perspectiva del cuerpo en el espacio sobre el plano del cuadro, y otras tres que le llamaremos proyecciones previas o proyecciones de proyecciones. Estas proyecciones se encuentran sobre el plano del cuadro.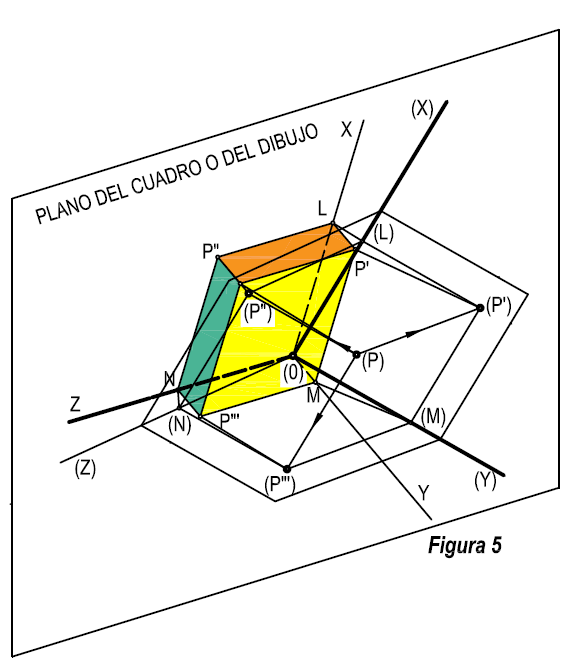
Como puede observarse en la figura 6, una vez girados los ejes hasta ocupar la posición con la habitualmente trabajamos, la recta PP’, es paralela al eje Z, la PP”, al eje Y, y la PP”, al eje X, tanto en el espacio como en proyección.
1.5. TRIANGULO DE TRAZAS.
Es la intersección del plano de proyección con las tres caras del triedro. Vamos a demostrar lo siguiente:
- Si trazamos distintos planos de proyección, los triángulos de trazas serán semejantes.
- Una proyección no depende del triangulo de trazas, si no, de la posición que ocupa el plano del cuadro.
- La alturas de un triángulo de trazas son los ejes del sistema.
- El triangulo de trazas será siempre acutángulo.
- Las bisectrices del triangulo órtico serán los ejes del sistema.
Consideremos un triedro trirrectángulo con el vértice hacia arriba, y lo cortamos por un plano paralelo al cuadro, Figura 7. Los segmentos AB = π3, AC = π2 y BC = π1, serán las trazas, intersección del triedro con un plano paralelo al cuadro. Si repetimos esta operación con otro plano cualquiera paralelo al cuadro, observaremos que los triángulos de trazas serán semejantes.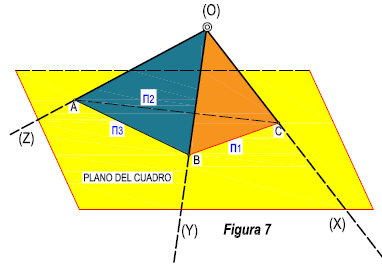
De acuerdo con lo anterior, el triángulo de trazas estará determinado por la posición que ocupe del plano de proyección con respecto al triedro. Por tanto la proyección no depende del triángulo de trazas.
Consideremos el plano paralelo al cuadro como plano de proyección, y proyectemos ortogonalmente, tendremos que los puntos A, B, C, intersección de las trazas del cuadro con los ejes se proyectan sobre si mimo, ( puntos dobles), y el vértice (O), se proyecta en O, perpendicular trazada al plano del cuadro. Las rectas que unen O con A, B, C, serán las proyecciones de los ejes (X), (Y), (Z), sobre el plano de proyección, que le denominaremos, X, Y, Z.
De acuerdo con el teorema de las tres perpendiculares, que dice “ si dos rectas en el espacio (Z) y , π1 son perpendiculares en el espacio y una de ellas π1, es paralela a un plano ( plano de proyección), sobre el cual se proyecta el conjunto ortogonalmente, se obtienen dos rectas Z y π1, que son perpendiculares entre si. ( hemos considerado que π1 se proyecta sobre si mismo). Igualmente aplicaríamos los ejes X, Y.
Por tanto podemos enunciar que los ejes de un sistema axonométrico, son las alturas del triángulo de trazas y serán perpendiculares a los lados de dicho triángulo.
Al proyectar una figura sobre el plano del cuadro, esta será ligeramente más pequeña. Esta diferencia estará en función del ángulo que forme el plano del cuadro con los ejes del sistema, (α, β, γ), (figura 8). Este valor será el coeficiente de reducción del sistema.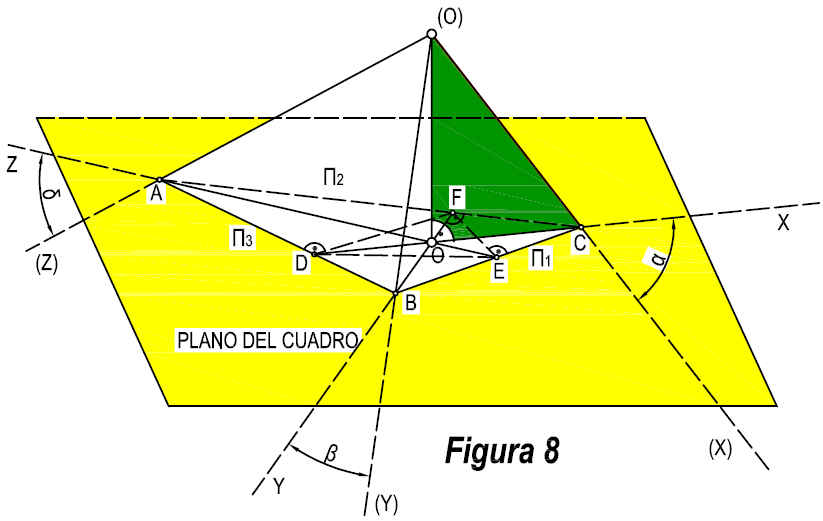
Para estudiar estos coeficientes con mayor simplicidad, consideremos un eje del sistema por separado. (Figura 9). El ángulo que forma en este caso el eje (X), y su proyección sobre el cuadro le llamamos α, al eje en el espacio le designamos por (X), y su proyección sobre el cuadro por X.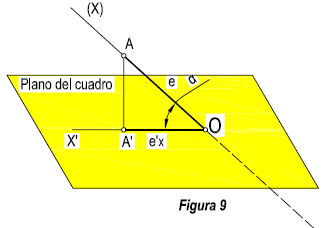
En la figura, se verifica que:
A’O = AO cos α, en donde,
AO es igual a la verdadera magnitud a proyectar. A’ O es la proyección sobre el plano del cuadro de la magnitud AO y
cos α , es el coeficiente de reducción ( ángulo que forma el eje con el plano del cuadro). Tendremos pues, tres coeficientes de reducción, cuyos valores serán cos α, cos β y cos δ.
Por tanto cualquier magnitud e tomada sobre el eje X, nos dará al proyectarse sobre el plano del cuadro, el valor ex, la relación entre ambos valores es lo que se conoce como coeficiente de reducción para el eje X, al cual le designaremos por Cx. Aplicando el mismo razonamiento para los tres ejes tendremos:
ex/e = Cx ey/e=Cy ez/e=Cz
Por tanto en el sistema axonométrico existirán tres coeficientes de reducción, uno por cada eje del sistema.
1.7. ESCALAS AXONOMÉTRICAS
Análogamente y basándonos en los coeficientes de reducción obtendremos las escalas axonométricas, entendiendo estas, como la proyección de la unidad e, referida a los ejes axonométricos.
De acuerdo con la figura 9, y haciendo la misma consideración para los ejes Y, Z, tendremos:
En la figura 9, haciendo OA = e y tomando sobre los ejes el mismo valor e = 1, se deduce que las unidades reducidas serán ex, ay, ez, sobre los ejes, equivalen a los ángulos α, β, λ.
De acuerdo con lo anterior, hay que tener en cuenta que una escala no es el coeficiente de reducción.
1.8. TEOREMA DE SCHLÖMILCH- WAISBASCH
Enunciamos este teorema en dos partes, sin entrar demasiado a fondo.
a) las proyecciones ortogonales de los ejes del triángulo sobre el plano cuadro, son las bisectrices del triángulo órtico.
b) Los cuadrados de las escalas axonométricas y la natural e. son respectivamente proporcionales a los lados y semiperímetro del triángulo órtico del de referencia.
ex2/ a = ey2/b = ez2/c = e2/p
siendo a, b, c, los lados del triángulo órtico, y p, el semiperímetro.
Si se cumple que dicho triángulo órtico es equilátero ( caso del sistema isométrico), tendremos:
a + b + c = P = 2p de donde:
(ex2 + ey2 + ez2 ) / (a + b + c) = e2 /p
ex2 + ey2 + ez2 =2e, o lo que es igual
cos2 α+ cos2 β+ cos2 λ = 2e
Si se trata del sistema isométrico, los ángulos que forman los ejes con el plano del cuadro son iguales, por lo que se cumplirá:
cos2 α = cos2 β = cos2 λ = cos2 γ de donde
cos2 α + cos2 β + cos2 λ = 3 cos2 γ = 2e de donde
cos2 γ = 2/3e
cos γ = 
Coeficiente de reducción en el sistema isométrico, como se verá más adelante.
1.9. RELACIONES ENTRE EL TRIÁNGULO DE TRAZAS, LOS COEFICIENTES DE REDUCCIÓN Y LAS ESCALAS AXONOMÉTRICAS.
Conociendo una cualquiera de las relaciones anteriores quedan determinadas las otras dos. Para una mayor claridad resolvamos algunos ejercicios.
Ejercicio 1.-Dado un triángulo de trazas determinar.
a) La dirección de los ejes coordenados, proyectados sobre el cuadro.
b) Determinar los ángulos que forman los ejes con el plano del cuadro. ( coeficientes de reducción)
c) Hallar las escalas de reducción y la natural, en cada uno de los ejes, y construir la escala volante.
Para resolver la primera parte del ejercicio, tendremos que aplicar la propiedad que dice “ las proyecciones de los ejes coordenados coinciden con las alturas del triángulo de trazas”, por tanto por cada uno de los vértices del triángulo de trazas P, Q, R, trazamos perpendiculares al lado opuesto, quedando definidos los ejes. (Figura 10).
Para determinar la segunda parte del ejercicio, se secciona el triedro por un plano proyectante que pase por cada uno de los ejes, y a continuación se abate la sección producida. Esta sección abatida nos dará el verdadero valor del ángulo de cada eje con los planos de proyección.
Para hallar la escala de reducción, ex se sitúa en la recta PR el valor real ( escala natural) y se trazan paralelas hasta que corte a la recta AD, el segmento ex , será el buscado. De la misma forma se actúa para el resto de los ejes.
Seguidamente pasamos a hallar el valor de las escalas métricas, que nos servirán para la construcción de una escala volante.
Tengamos el segmento VM, dividido en cm. de la escala natural, tomando como vértice el punto V, se construyen los ángulos hallados anteriormente α = 34º, β = 44º, λ = 28º, y en la disposición indicada en la figura 11. Llevamos sobre el lado ex, ey, ez, divisiones de 10 mm. Por cada una de ellas, se trazan perpendiculares a los lados e de los ángulos construidos, que nos determina la escalas métricas correspondientes.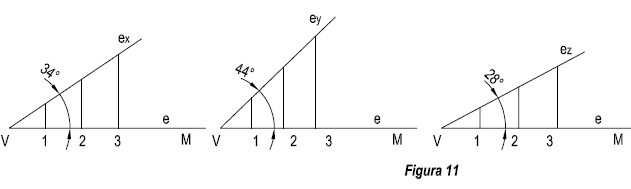
Ejercicio 2.- Dados los ángulos α = 30º, λ=38º, determinar los ejes axonométricos.
Trazamos una recta vertical que nos determina la dirección del eje Z, haciendo centro en un punto cualquiera (G), se traza una semicircunferencia, con un radio cualquiera. Por el punto N, trazamos una recta perpendicular, seguidamente por el extremo M, se traza una recta que forme un ángulo λ con el eje Z, hasta que corte a la semicircunferencia en Oo, por donde se traza una perpendicular a MN, que nos determina el vértice del triedro. El ángulo O N Oo = λ, será el que forme el plano XOY con el cuadro.
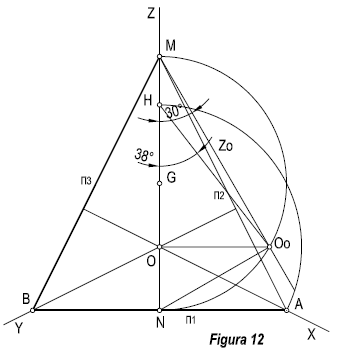
Por tanto la recta π1, trazada por N, será la traza del plano XOY que buscamos. Por Oo, trazamos una recta que forme con el eje Z, el ángulo α= 30º dado, obteniendo el punto H. Con centro en O y radio OH, trazamos un arco que corte a π1 en A; la recta OA, es la proyección del eje X, y por tanto AM, es la traza α2 del plano con XOZ. La proyección del eje Y, pasa por O y es perpendicular a π2, la traza π3 pasa por B y es perpendicular al eje X.
Muface