| Utiles | Trazados Fund. | Triángulos | Polígonos | Igualdad y Semejanza |
|---|---|---|---|---|
| Potencia. Eje Radical | Homologia y Afinidad | Tangencias | Enlaces, Óvalos, Espirales | Cónicas |
a) Construcción de un cuadrado regular dado el lado. Fig. 86.
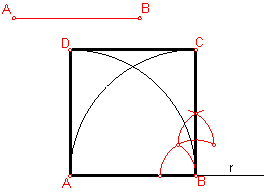
Sea el lado AB:
Sobre una recta r cualquiera, llevamos el valor del lado dado.
Por el extremo A y B, levantamos dos perpendiculares.
Haciendo centro en A y B traza dos arcos hasta que corten a las perpendiculares anteriores, obteniendo los vértices C y D.
b) Cuadrado regular, dada la diagonal. Fig. 87.
La diagonal del cuadrado coincide con el radio de la circunferencia circunscrita.
Con centro en O, trazamos la circunferencia circunscrita.
Seguidamente, trazamos sus diámetros ortogonales obteniendo los puntos A, B, C, D.
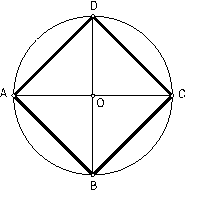
Fig. 87
Uniendo los puntos A, B, C, D, tenemos la solución.
1.2. Rectángulo
a) Construcción de un rectángulo dada el lado y la diagonal. Fig. 88.
Bastará con construir dos triángulos rectángulos, dada la hipotenusa y un lado.
Sobre una recta r, llevamos el valor del lado AB.
Por el extremo B levantamos una perpendicular.
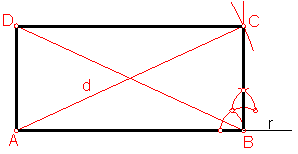
Fig. 88
Haciendo centro en A y con radio el valor de la diagonal d, trazamos un arco, obteniendo el vértice C.
Repetimos la operación en el punto A.
a) Construcción de un rombo dada la diagonal y un lado. Fig. 89.
Sea el lado AB y la diagonal d:
Será preciso construir el triángulo isósceles dado por la diagonal y el lado. ( dos datos).
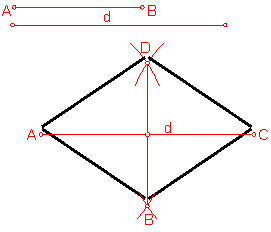
Fig. 89
Trazamos la mediatriz de la diagonal dada d.
Haciendo centro en los extremos A y B trazamos dos arcos con el valor AB que determinan los vértices C y D.
1.4. Romboide
a) Construcción de un romboide dado dos lados y la diagonal. Fig. 90.
Sean los lados AB y BC, y la diagonal d.
Como la diagonal divide al romboide en dos triángulos escálenos. Bastará con construir dicho triángulo conociendo tres de lados.
Sobre una recta llevamos el valor del lado AB.
Con centro en A trazamos un arco de radio el valor de la diagonal d.
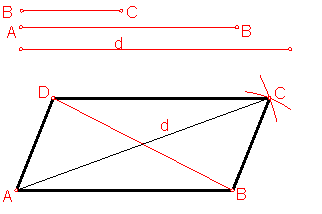
Fig, 90
Con centro en B, repetimos la operación con el valor del lado BC, obteniendo el vértice C.
La unión de ABC determina uno de los triángulos. Repitiendo la operación tendremos el otro.
b) Construcción de un romboide dado dos lados y el ángulo que forman. Fig. 91
Sea el ángulo A y los lados AB y BC:
Bastará con construir un triángulo escaleno conociendo dos lados y el ángulo comprendido.
Sobre una recta r y en su extremo, construimos el ángulo A.
Con centro en A y radio AB trazamos un arco punto B.
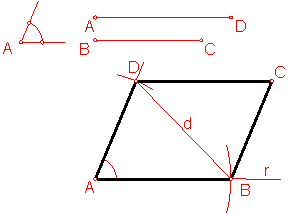
Fig. 91
Con centro en A y radio AD trazamos otro arco, punto D.
La unión de ABD, determina uno de los triángulos.
El otro se halla de forma similar.
c) Construcción de un romboide dado dos lados a y b y el ángulo menor de las diagonales que vale 75º ( opuesto al lado dado a). Fig. 92.
Resolveremos el ejercicio por medio de arco capaz, teniendo en cuenta que el lado b es paralelo a la mediana ma del triángulo formado por el lado a y el ángulo que forman las diagonales.
Sobre una recta llevamos el lado a.
Construimos el arco capaz de 75º.
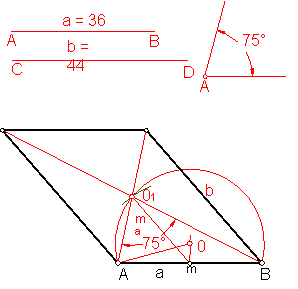
Fig. 92
Con centro en m y radio la mitad del lado b, (mediana del triangulo buscado) trazamos un arco que determina el punto O1.
La unión de A, B, O1, nos determina el triangulo que forma las diagonales y el lado a.
Prolongamos la diagonal A O1. y con centro en B y radio b, trazamos un arco, obteniendo teniendo el vértice C.
Mediante paralelas completamos el ejercicio.
a) Trapecio rectángulo conociendo la base mayor la altura y el ángulo
que forma dicha base con el lado. Fig. 93.
Sea b la base mayor, h la altura y α el ángulo que forma la base mayor con el lado b.
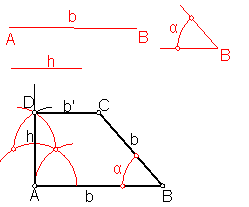
Fig. 93
Sobre una recta llevamos la base mayor b.
En el extremo A levantamos una perpendicular h.
Llevamos sobre dicha perpendicular el valor h dado, punto D.
En el extremo B, trasladamos por medio del compás el ángulo α.
Por D trazamos una paralela a la base mayor, obteniendo el vértice C.
b) Trapecio rectángulo conociendo la base mayor b la altura h y la diagonal d. Fig. 94.
Sea b la base mayor, h la altura y d la diagonal.
Sobre una recta llevamos la base mayor b.
En el extremo A levantamos una perpendicular h.
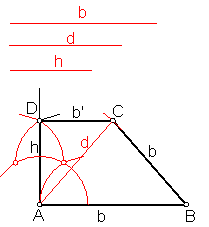
Fig. 94
Llevamos sobre dicha perpendicular el valor h dado, punto D.
Por D trazamos una paralela b’ a la base mayor b.
Haciendo centro en A y con el valor de la diagonal d trazamos un arco que corta a b’ en C.
c)Trapecio isósceles dada la base mayor b la media bm y la altura h. Fig. 95.
Sea b la base mayor y bm la media y h la altura.
Hallamos la mediatriz de b y a partir de 3 llevamos h.
Hallamos la mediatriz de h.
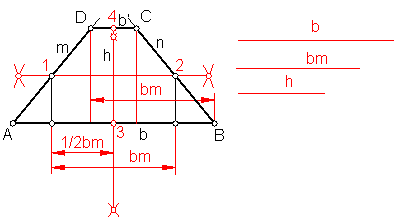
Fig. 95
Llevamos a partir de 3 a cada lado ½ bm y levantamos dos perpendiculares hasta que corte a la mediatriz en los puntos 1-2
Unimos A con 1 y B con 2
A partir de A y B llevamos el valor de la bm.
Levantamos dos perpendiculares que cortarán a las rectas m y n en los puntos C y D.
d) Trapecio escaleno dadas las dos bases b y b’ y los dos ángulos adyacentes a la base mayor. Fig. 96.
Sean b la base mayor, b’ la menor, y A y B los ángulos adyacentes a la base mayor.
Llevamos sobre una recta el valor de la base mayor b.
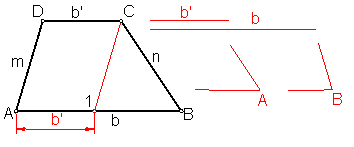
Fig. 96
En sus extremos construimos por medio del compás los ángulos dados A y B
A partir de A llevamos el valor de la base menor.
Por el punto 1 trazamos una paralela a la recta m que corta a la n en C.
La unión de D y C nos determina el trapecio.
e) Trapezoide dados los cuatro lados y la altura correspondiente a uno de ellos. Fig. 97.
Sean los lados a, b, c y d y la altura ha.
Sobre una recta llevamos el valor del lado a.
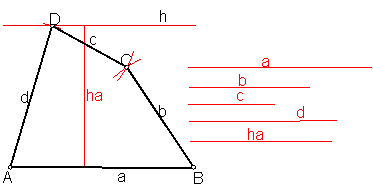
Fig. 97
En un punto cualquiera de ella, trazamos una recta perpendicular, llevando el valor correspondiente a la altura ha.
Con centro en A, y radio el valor del lado d, trazamos un arco que cortará a la paralela h en el punto D.
Con radio c, y haciendo centro en C, trazamos un arco.
Con centro en B y radio B, trazamos otro arco. Ambos se cortan en el vértice C. La unión de todos ellos nos determinan el trapezoide.
2.1. Construcción de polígonos dado el radio de la circunferencia circunscrita
El triángulo y el cuadrado han sido visto con anterioridad, por tanto comenzaremos por aquellos superiores a 4 lados.
a) Hexágono regular dado el radio de la circunferencia circunscrita Fig. 98.
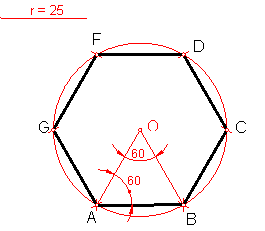
Fig. 98
Tendremos en cuanta que el valor del lado es igual al radio r de la circunferencia.
b) Pentágono regular dado el radio de la
circunferencia circunscrita. ( procedimiento exacto). Fig. 99.
Con centro en O, trazamos la circunferencia
circunscrita y seguidamente sus diámetros
ortogonales A, B, C, D,
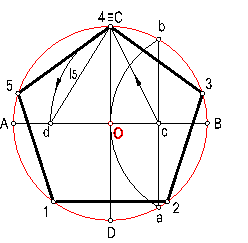
Fig. 99
Hallamos la mediatriz del radio, punto c.
Hacemos centro en c y con radio cC, trazamos
el arco Cd.
La distancia dC, será L5, lado del pentágono.
c) Heptágono regular dado el radio de la circunferencia circunscrita. (procedimiento aproximado). Fig.100.
Con centro en O, trazamos la circunferencia
circunscrita y seguidamente sus diámetros
ortogonales,
Hallamos la mediatriz del radio, punto c.
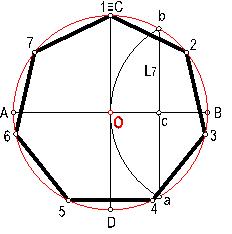
Fig. 100
El segmento cb, será el lado L7.
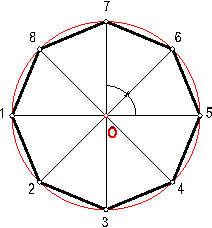
Fig. 101
d) Octógono regular, dado el radio de la circunferencia circunscrita. Fig. 101.
Con centro en O, trazamos la circunferencia
circunscrita, seguidamente, sus diámetros ortogonales, 1-2 y 3-7.
Hallamos la bisectriz de los ángulos de 90º, obteniendo el resto de los puntos.
e) Decágono regular dado el radio de la circunferencia circunscrita. Fig. 102.
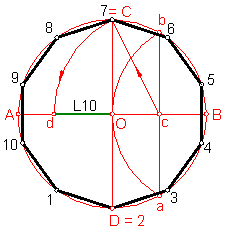
Fig. 102
Su construcción es similar al pentágono.
Con el valor del radio trazamos una circunferencia.
Hallamos la mediatriz del radio, OB punto c.
Con centro en c y radio c C, trazamos un arco, punto d.
La distancia dO, será el valor del lado buscado.
f) Eneágono dado el radio de la circunferencia
circunscrita. Fig. 103

Fig. 103
Trazamos la circunferencia de centro O.
Con centro en CD trazamos dos arcos con el valor del radio. Puntos a y b.
Con centro en C y D trazamos dos arcos con el valor Cb y Da, obteniendo el punto M.
Haciendo centro en M trazamos un arco con el valor de MC, obteniendo la recta dA, que será el lado buscado L9.
g) Procedimiento general de construcción de polígonos dado el radio de la circunferencia circunscrita. Fig. 104.
Dividir una circunferencia dada en 15 partes y construir el pentadecágono correspondiente.
Trazamos la circunferencia con el radio dado y sus ejes perpendiculares.
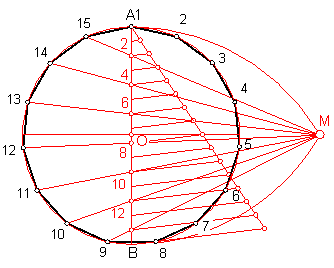
Fig., 104
Dividimos el diámetro en 15 partes iguales.
Hacemos centro en los extremos A y B y trazamos dos arcos con el valor del diámetro, ambos se cortan en el punto M.
Unimos M con las divisiones pares, obteniendo los puntos del 9 al15.
Para obtener el resto e los puntos podemos repetir la operación, uniendo los puntos impares, o bien llevar el lado obtenido. En este último caso la precisión es menor.
2.2. Construcción de polígonos dado el lado
a) Pentágono dado el lado. Fig. 105.
Tendremos en cuenta que el lado del pentágono y su diagonal están en relación áurea. Por tanto su valor será 1,618.
Sobre una recta r llevamos el valor del lado.
Hallamos su mediatriz GD.
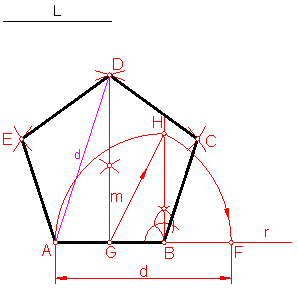
Fig. 105
Levantamos una perpendicular en el extremo B.
Llevamos sobre dicha perpendicular el valor del lado L, punto H.
Haciendo centro en G y radio GH trazamos un arco punto F.
La distancia AF será la diagonal del pentágono.
Con centro en A y B y valor la diagonal d, trazamos dos arcos, punto D. Con el valor del lado se completa el ejercicio.
c) Construcción del heptágono dado el lado. Fig. 106.
El procedimiento es aproximado. Consiste buscar el centro de la circunferencia en la que queda inscrito el polígono.
Sobre una recta r llevamos el valor del lado AB.
Trazamos su mediatriz y levantamos una perpendicular por el extremo B.
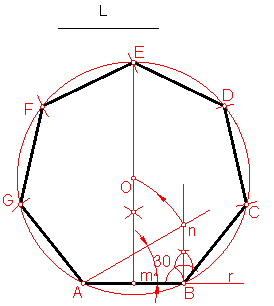
Fig. 106
En el extremo A construimos un ángulo de 30º determinando el punto n.
Haciendo centro en A y radio An trazamos un arco que no fija en centro O de la circunferencia buscada.
Sobre esta circunferencia llevamos el valor del lado.
d) Construcción del octógono dado el lado. Fig. 107.
Como en los casos anteriores hallaremos el centro de la circunferencia circunscrita.
Construimos un cuadrado que tenga por valor el lado del octógono L.
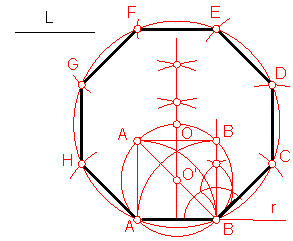
Fig. 107
La diagonal del cuadrado corta a la perpendicular en el punto medio del lado en O’.
Con centro en O’ trazamos una circunferencia que nos da el centro O.
El resto del ejercicio es similar a los casos anteriores
e) Construcción del decágono dado el lado Fig. 108..
Construiremos un pentágono que tenga por valor el del lado del decágono.
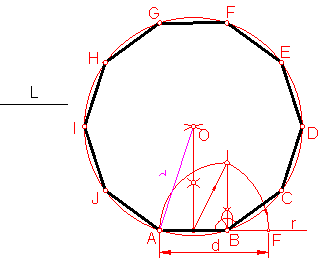
Fig. 108
La diagonal de dicho pentágono nos determinara el centro O.
ff) Construcción del eneágono dado el lado ( construcción aproximada) Fig. 109.
Sobre una recta r llevamos el valor del lado L.
Trazamos su mediatriz.
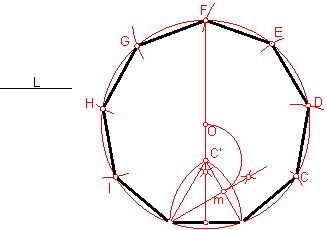
Fig. 109
Construimos el triángulo equilátero ABC’. Seguidamente hallamos su bisectriz que corta a uno de los lados del triángulo en el punto m.
Con centro en C’ y radio C’ m, tramos un arco que nos determina el punto O, centro de la circunferencia circunscrita al polígono. Se completa el ejercicio llevando el valor del lado sobre la circunferencia.
g) Por el procedimiento, general dibujar un polígono regular de 11 lados, dado el lado. Fig. 110.
El ejercicio se resuelve por semejanza.
Sea el lado 1-11,
Con centro en O, construimos un polígono cualquiera de 11 lados.
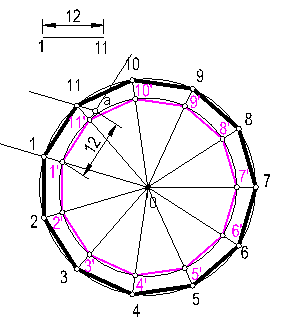
Fig. 110
Sobre uno de los lados, el 1’-11’, llevamos el lado dado 1-11. Punto a.
Por el punto a, trazamos una paralela al radio 1’-0, hasta que corte a la prolongación del radio, 0-11’ en 11.
Trazando paralelas por 11 a los lados del polígono auxiliar obtendremos la solución.
Polígono regular estrellado, es aquel que se cierra después de recorrer más de una vez la circunferencia.
Para hallar los estrellados de un polígono tendremos en cuenta lo siguiente:
Numero de lados del polígono, de ellos hallaremos aquellos que sean menores que la mitad de ellos. Por último elegiremos todos aquellos que sean primos el el número de lados.
Por ejemplo: a) Hallar el polígono estrellado del eneágono. Fig. 111.
Número de lados 9
Números enteros menores que la mitad de los lados 1, 2, 3, 4
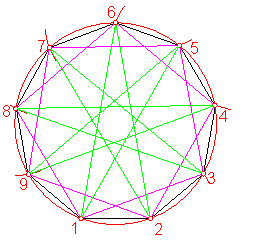
Fig. 111
Números primos con 9 2 y 4
De ello se deduce que el eneágono tiene dos estrellados. Uniendo los vértices de 2 en 2 y de 4 en 4.
b) Heptágono estrellado. Fig. 112
Número de lados 7
Números enteros menores que la mitad 1, 2, 3
Números primos con 7 2,3
Este será el orden de unión de los vértices.
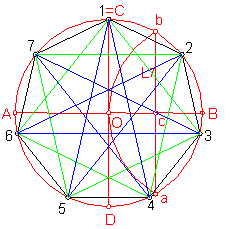
Fig. 112


