| Utiles | Trazados Fund. | Triángulos | Polígonos | Igualdad y Semejanza |
|---|---|---|---|---|
| Potencia. Eje Radical | Homologia y Afinidad | Tangencias | Enlaces, Óvalos, Espirales | Cónicas |
Trazados Fundamentales en el Plano
1) Introducción
Denominamos punto al cruce de dos líneas, este no tiene dimensión. En lo sucesivo lo denominaremos por letras mayúsculas.
Una línea es una sucesión ilimitada de puntos. Cuando estos van en la misma dirección
definen una recta. La denominaremos por una letra minúscula.
Si la recta está limitada en uno de sus extremos, estaremos definiendo una semirrecta.
Si se encuentra limitado por los dos extremos será un segmento.
Lugar geométrico en el conjunto de puntos que cumple una determina condición.
Si dos rectas se cortan formando un ángulo de 90º, estas serán perpendiculares.
2.1. Rectas perpendiculares. Definición
Dos rectas son perpendiculares cuando se cortan formando ángulos rectos. Dos rectas perpendiculares formarán por tanto cuatro ángulos rectos.
2.2. Trazado de la perpendicular a un segmento en su punto medio. Mediatriz de un segmento. Fig.12.
La mediatriz de un segmento es el lugar geométrico de los puntos equidistantes de sus extremos a y b y por tanto es la perpendicular en su punto medio.
Sea el segmento A-B.
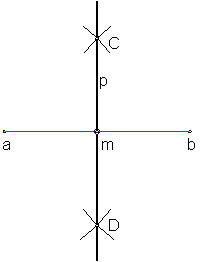
FIg. 12
Con centro en A y con radio mayor que la mita del segmento ( 2/3 aproximadamente), se trazan dos arcos de circunferencia.
Con el mismo radio y haciendo centro en B se traza otros dos arcos que cortarán a los anteriores en los puntos C y D.
La unión de los puntos anteriores nos determinan la recta p, mediatriz
del segmento AB. Esta será el lugar geométrico de todos los puntos que
equidistan de los extremos del segmento a y b.
2.3.Trazado de la perpendicular a una recta en un punto de ella. Fig.13.
Sea la recta r y un punto de la misma P.
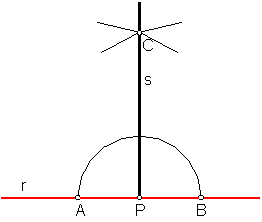
Fig. 13
Con centro en P y radio arbitrario se traza una semicircunferencia que nos determinan los puntos A y B.
El caso queda reducido al primero de los explicados.
2.4. Trazado de la perpendicular a una recta desde un punto exterior. Fig.14.
Sea la recta s y un punto exterior a ella Q.
Con centro en Q y radio mayor que la distancia de Q a r, se traza un arco que cortará a la recta en los puntos A y B.
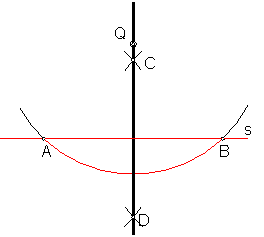
Fig. 14
El problema queda reducido al caso primero.
2.5. Trazado de la perpendicular a una recta en su extremo. Fig.15
Con centro en el extremo A y con radio arbitrario trazamos un arco que corte a la recta r en el punto B.Primer procedimiento: Sea la semirrecta r y su extremo A.
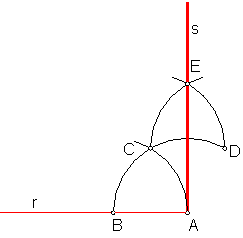
Fig. 15
Manteniendo el mismo radio y con centro en B, C y D, trazamos tres arcos que nos determinan el punto E.
La unión de E con A, será la perpendicular s buscada.
Segundo Procedimiento: Sea la semirrecta r y su extremo P. Fig.16.
Se determina C como en el caso anterior.
Se une B con C, y se prolonga.
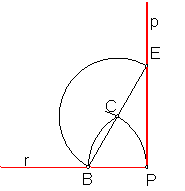
Fig. 16
Con centro en C, trazo un arco con de radio de BC, obteniendo el punto E. La unión de PE, determina la solución p.
Tercer Procedimiento: Sea la semirrecta r y su extremo A. Fig.17
Elegimos un punto cualquiera C, exterior a r y haciendo centro en el, trazamos un arco que pase por P. y corte a r en B.
Unimos B con C, y prolongamos la semirrecta hasta que
corte a la circunferencia en E.
La unión de E con P, será la perpendicular s buscada.
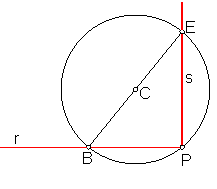
Fig. 17
En definitiva lo que hemos realizado ha sido un triángulo
rectángulo con uno de sus catetos en la semirrecta r.
2.6. División de un arco de circunferencia en dos partes iguales. Fig.18.
Es una aplicación del ejercicio, mediatriz de un segmento.

Fig. 18
Sea el arco AB.
Se une A con B y seguidamente trazamos la mediatriz de dicho segmento.
2.7. Dados tres puntos que no estén en línea recta, hallar la circunferencia que pase por ellos. Fig.19.
Sean los puntos A, B, C.
Unimos A con B y B con C.
Hallamos la mediatriz de a ambos de ambos segmentos.
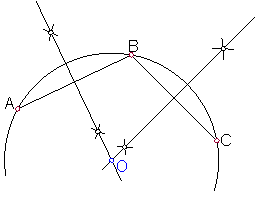
Fig. 19
Se llaman rectas paralelas a aquellas que situadas en un mismo plano, no se encuentran por más que se prolonguen en ambas direcciones.
3.1. Teorema
Si dos rectas son perpendiculares a una tercera, estas son paralelas entre si, de los contrario se cortarían en un punto desde el cual podría trazarse dos perpendiculares a una misma recta.
3.2. Distancia entre dos rectas paralelas.
Es el segmento de perpendicular a ambas comprendido entre ellas, que por lo dicho segmento será siempre igual cualquiera que sea el punto por donde se trace.
3.3. Trazado de una paralela a una recta que pase por un punto exterior.
3.3.1. Primer procedimiento. Fig. 20.

Fig. 20
Sea la recta t y el punto exterior a ella P.
Elegimos un punto cualquiera en la recta r, por ejemplo el punto A.
Trazamos una semicircunferencia que pase por el punto dado P,
Determinando en la recta r, los puntos B y C.
Trasladamos la cuerda BP, para ello con centro en B y radio BP, se traza un arco, que corta a la semicircunferencia en el punto D.
La unión de D con P, será la recta buscada.
3.3.2. Segundo procedimiento. Fig.21.
Segundo Procedimiento:
Haciendo centro en un punto cualquiera de la recta r, por ejemplo en A, trazamos un arco de circunferencia que pase por P, determinando los punto B y C.
Por medio del compás, tomamos la distancia de CP, y
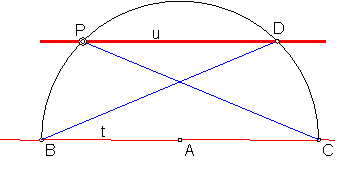
Fig. 21
la llevamos a partir de B, obteniendo el punto D.
La unión de D con P, será la recta buscada.
3.3.3. Tercer procedimiento. Fig. 22.
Basta con considerar que dos rectas que se encuentran
en un mismo plano que son perpendiculares a una
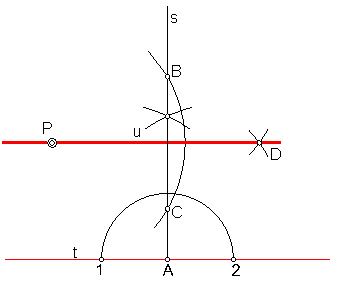
Fig. 22
tercera, son paralelas entre si.
Elegimos un punto cualquiera en la recta t, el A, y
trazamos una recta perpendicular.
Seguidamente trazamos una recta u perpendicular
a s que pase por un punto exterior P., visto anteriormente.
4) Paralelismo y perpendicularidad por medio de plantillas.
4.1. Rectas paralelas.
Para el trazado de paralelas con plantillas debemos seguir los pasos siguientes:

Fig. 23

Fig. 24
Segunda posición: Manteniendo inmóvil la escuadra con la mano izquierda, ( para diestros), situar la hipotenusa del cartabón pegada a uno de los lados de la escuadra. Fig.24.
Tercera posición: Sin mover ahora el cartabón, deslizamos la escuadra para el trazado de horizontales. Fig.25

Fig. 25
4.2.Rectas perpendiculares. Fig.26.
Partiendo de la posición tercera, giramos la escuadra 90º.
Y la deslizamos apoyada en la hipotenusa del cartabón.
Fig. 26
5.1. Definiciones
Denominamos ángulo plano convexo a la porción de espacio comprendida entre dos semirrectas a y b que se cortan en un punto V que es el vértice del mismo.
Se llama ángulo llano, al definido por dos semirrectas opuestas. Fig.27.

Fig. 27
Se llama ángulo adyacente, al contiguo, cuyos lados no comunes son semirrectas opuestas. Su suma es un ángulo llano. Este ángulo también se llama suplementario. Fig.28.
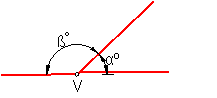
Fig. 28
Dos ángulos opuestos por el vértice son iguales. Fig. 29
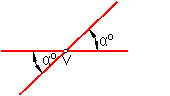
Fig. 29
Se llaman ángulos complementarios, a aquellos que su suma vale un recto. Fig.30.
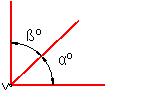
Fig. 30
5.2. Trazado de un ángulo igual a otro. Fig. 31.
La construcción de un ángulo igual a otro, se fundamenta en que ángulos iguales le corresponden arcos y cuerdas iguales.
Sea el ángulo A.
Sobre la recta s, tomamos un punto cualquiera V.
Con centro en V trazamos un arco con radio arbitrario.
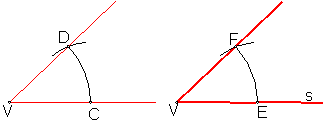
Fig. 31
Manteniendo el mismo radio, trazamos otro igual por V’.
Con la cuerda CD, trazamos el arco EF.
Uniendo V’ con F, tendremos el mismo ángulo.
5.3. Suma de ángulos. Fig.32
Para sumar dos ángulos bastará con repetir la operación anterior tantas veces como ángulos queramos sumar, siempre en el mismo sentido.
Sean los ángulos A y F.
Con centro en A, F y G, se trazan tres arcos iguales con radio arbitrario.
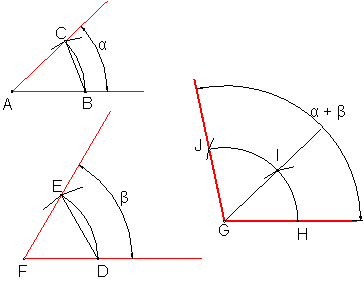
Fig. 32
Por medio del compás llevamos la cuerda BC, a partir de H, obteniendo el punto I.
Realizamos la misma operación con la DE, que llevamos a partir de I, obteniendo el punto J, que unido con G. tendremos la solución.
5.4. Diferencia de ángulos. Fig.33.
El ejercicio es similar al anterior, con la diferencia que las cuerdas se llevarán en sentido contrario a partir de un punto común.
Sean los ángulos A y B y la semirrecta s.
Trazamos con un radio arbitrario tres arcos de circunferencia iguales con centro en A, B, y V.
Por medio del compás llevamos la cuerda mayor CD, sobre G, obteniendo el punto H.
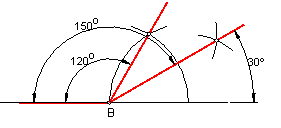
Fig. 33
Restamos del arco anterior la cuerda EF,
obteniendo el punto I. Uniendo I con V nos
da la solución.
5.5. Bisectriz de un ángulo.
Se llama bisectriz de un ángulo a la línea que los divide en dos partes iguales.
Sea el ángulo A.
Con centro en A trazamos un arco de radio arbitrario BC. Conviene que el radio no sea muy pequeño. Fig.34.
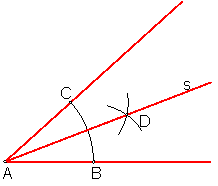
Fig.34
Hallamos la mediatriz de la cuerda BC, obteniendo el punto D.
La recta s, será la bisectriz del ángulo
Podemos utilizar un segundo procedimiento ( Fig.35) que se describe a continuación.
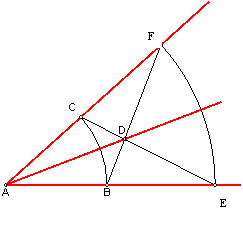
Fig. 35
Haciendo centro en el vértice A, trazamos dos arcos de radio arbitrario. Unimos los puntos B – F y E –C. La bisectriz será la recta AD.
5.6. Bisectriz de un ángulo de vértice desconocido. Fig.36.
Sea el ángulo formado por las rectas r y s.
Trazamos una recta p, arbitraria, que determina con las rectas anteriores los ángulos 1, 2, 3, 4.
Por el procedimiento anterior, hallamos las bisectrices de dichos ángulos, que se cortan en los puntos A y B, puntos de la bisectriz buscada.
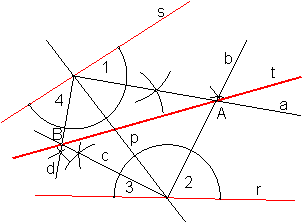
Fig. 36
5.7. Trazados de ángulos por medio del compás.
Ángulos de 90º y 45º. Fig.37.
Bastará con trazar un perpendicular en el punto A, seguidamente hallar su bisectriz.
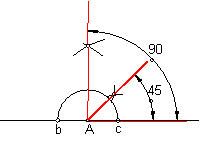
Fig. 37
Con la bisectriz del mismo obtendremos el de 30º.Ángulos de 60º y 30º. Fig.38.
Elegimos un punto cualquiera A, con un radio arbitrario trazamos un arco, obteniendo el punto B.
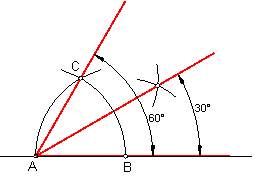
Fig. 38
Haciendo centro en B y con el mismo radio, trazamos otro arco, obteniendo el punto C.
La unión de C con B nos determinará el ángulo de 60º.
Ángulos de 30º, 150º y 120º. Fig.39.
Construimos el ángulo de 60º, visto anteriormente.
Hallamos su bisectriz, con lo que tenemos el ángulo de 30º.
El suplementario de 30º será el ángulo de 150º.
El suplementario de 60º será el de 120º.

Fig. 39
5.8. Trazado de ángulos con la escuadra y el cartabón. Fig. 40,41,42.
Teniendo presente los ángulos que forman los lados de la escuadra y el cartabón
podemos combinar estos para obtener ángulos múltiplos y submúltiplos de ellos.
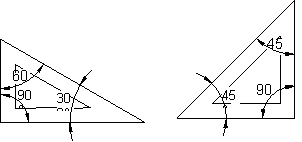
Fig. 40
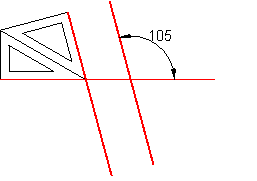
Fig. 41
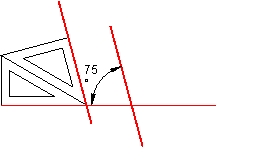
Fig. 42
5.9. Ángulos en la circunferencia.
Ángulo central β. Fig.43. Es aquel que tiene el vértice en el centro de la circunferencia O, y por lados los radios de la misma.

Fig. 45
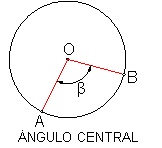
Fig. 43
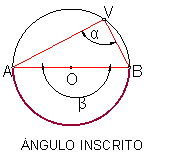
Fig. 44
Ángulo inscrito α. Fig.44- 45.
Tiene el vértice V en la circunferencia y sus lados son rectas secantes a ella. Su valor es la mitad del ángulo central que abarca el mismo arco.(α = β/2).
Ángulo seminscrito α. Fig.46.
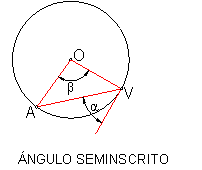
Fig. 46
Tiene el vértice V en el centro de la circunferencia y los lados son cuerda y tangente. Su valor es la mitad del ángulo central. ( α=β/2)
Ángulo exterior. Fig.47. Tiene por vértice un punto exterior
a la circunferencia y los lados son tangentes o secantes a la misma. Su valor será: (α = (β – φ)/2)

Fig. 47
Ángulo exterior α. Tiene por vértice V un punto exterior
a la circunferencia y los lados son tangentes o secantes a la misma. Su valor será: (α = (β – φ)/2).
Se denomina arco capaz de un segmento dado con respecto a un ángulo, al lugar geométrico de los puntos de una circunferencia desde los cuales se ve dicho segmento bajo el mismo ángulo. Fig. 48.
Construcción:
Sea el ángulo α = 42º y el segmento AB.
Sobre una recta cualquiera, llevamos el segmento AB.
Construimos en el extremo A el ángulo 90- 42º = 48.
Trazamos la mediatriz del segmento AB.
El punto O donde la recta m corta a la mediatriz p, será el centro del arco capaz.
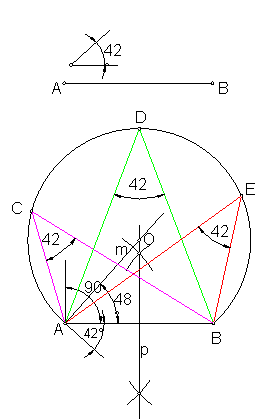
Fig. 48
Como puede observarse los ángulos C, D, E son iguales entre si y tienen por valor el α dado.
También puede resolverse trazando en el extremo A un ángulo de 42º, hacia abajo. La perpendicular a uno de sus lados nos determina el centro O.


