- Representación del Punto
1.1. Nomenclatura
Para la representación del punto utilizaremos, al igual que en el resto de los sistemas de representación, una letra mayúscula, principalmente las primeras del abecedario. Para la proyección horizontal utilizaremos la misma letra acompañada de una comilla y dentro de un paréntesis el valor de la cota. Para la representación del plano de proyección utilizaremos letras griegas. Para una mayor comodidad utilizaremos como unidades el centímetro. En topografía esta unidad es el metro.
1.2. Representación del punto
Este sistema de representación utiliza un solo plano de proyección, el plano horizontal, que recibe el nombre de plano de proyección, plano del cuadro o plano de referencia.
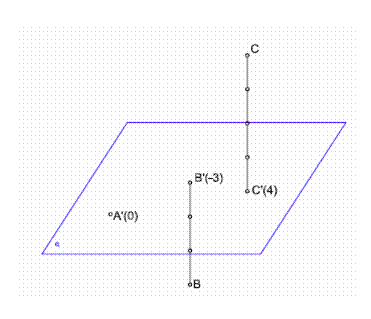
Figura 1
Los puntos pueden situarse en el plano horizontal, por encima o por debajo. Sea por ejemplo el punto C ( figura 1), que se encuentra a 4 unidades por encima del plano horizontal. Este quedará definido de la forma siguiente C’(4), que indica que se encuentra a 4 cm. por encima del plano horizontal.
El punto B, se encuentra por debajo del plano del cuadro, por tanto su cota será negativa B’ (-3). Hay que tener en cuenta que el plano de comparación o plano de cota cero se considera el nivel del mar a la altura de la playa del Postiguet en Alicante, en nuestro ejemplo el punto A’ (0).
Las cotas positivas de llaman altitudes y la negativas profundidades.
Se denomina desnivel de dos puntos o la diferencia algebraica existente entre ellos.
Por ejemplo el desnivel entre el punto A y C, será de 4 cm. El desnivel entre C y B será 4 – ( – 3) = 7 cm.
- 2. Representación de la Recta
2.1. Nomenclatura.
Para la representación de la recta utilizaremos letras minúsculas, principalmente, r, s o t. La proyección horizontal se representará por la misma letra acompañada de una comilla. Por ejemplo r’.
2.2. Proyecciones de la Recta.
Una recta quedará definida cuando se conozcan dos de sus proyecciones. En la figura 2, los puntos A’(1) y G’(6), nos definirán la recta.
Se denomina traza de una recta a la intersección de esta con el plano del cuadro. En la recta s, figura 2, la traza la representaremos por el punto T, este será un punto doble y por tanto coincidiera con su proyección T’, su cota será por tanto 0.
El triángulo TAA’=ABB’=CDD’
Si consideramos que AA’ = Bp…. = 1 cm, y aplicando el teorema de Thales, tendremos que TA/T’A’= AB/p=CD/Cq
El segmento Ap = Cq = i ( intervalo o modulo), que como puede apreciarse es la proyección de los segmentos AB, cuyo desnivel es la unidad.
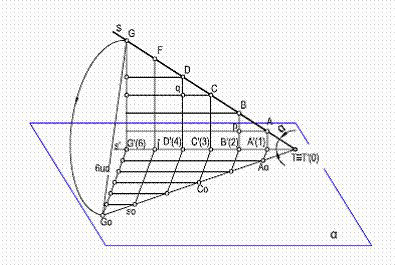
Figura 2
De la figura deducimos que la Tg =AA’/A’T = 1/A’T = 1/i = P, siendo P La pendiente de la recta.
Por tanto la pendiente de una recta será la inversa del intervalo.
Es decir la pendiente de una recta será la tangente que esta forme con el plano del cuadro. Siendo el desnivel de dos puntos la diferencia de sus cotas. En la figura 1, el desnivel entre el punto B’(2) y el D’(4) será de 2 unidades.
Esta pendiente puede venir expresada en tanto por ciento.
Si consideramos un tramo de carretera cuya pendiente sea del 10%, la proyección horizontal serán 100 metros mientas que la diferencia de alturas será de 10 metros. Aplicando la formula anterior Tg =AA’/A’T =10/100.
Del triángulo TAA’, tendremos que TA’ = A’A cos Por tanto la pendiente de la recta será el valor de la tangente que forma la recta con el plano de cuadro.
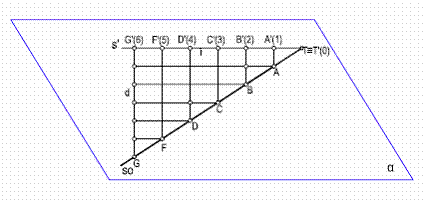
Figura 3
El desnivel d entre dos puntos será la diferencia de cotas.
Si abatimos la recta s sobre el plano del cuadro ( figura 3), tendremos la verdadera posición de la recta.
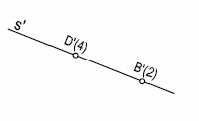
Figura 4
Graduar una recta, por ejemplo s’, es dividirla en tantas partes iguales como diferencia haya entre sus cotas. En la figura 4 tenemos una recta dada por los puntos B’(2) y D’(4), la diferencia de cotas es 2, por lo
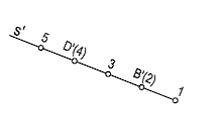
Figura 4a
tanto dividiremos en dos partes D’-B’ y ese valor será el intervalo i. Con ese valor tomaremos en la recta distintas divisiones con lo que esta quedará graduada, figura 2ª.
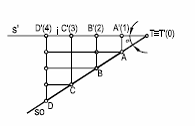
Figura 5
Si queremos obtener el ángulo que la recta forma con el plano de proyección, bastará con abatir la recta s’, para ello levantaremos una perpendicular por una de las divisiones, por ejemplo la nº 4, llevando sobre ella la unidad que hemos utilizado de medida, 4 centímetros. Uniendo el punto D con la traza del Plano T, tendremos la verdadera posición de la recta, así como el ángulo α que forma con el cuadro. Figura 5.
1.1. Alfabeto de la Recta
La recta puede ocupar en el espacio tres posiciones
a) Oblicua, recta que hemos visto anteriormente.
b) Paralela al plano de proyección.
c) Perpendicular al plano de proyección..
Como se ha visto con anterioridad la recta oblicua nos viene definida por dos puntos cualquiera de ella, p.e D’(4) y A’(1) . La paralela tendrá todas sus cotas iguales, por lo que se definirá por el valor de la cota p.e s’(6) y la perpendicular se definirá por su traza p.e. s’ . Figura 6.
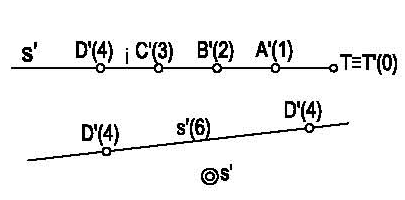
Figura 6
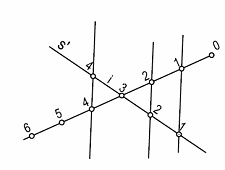
Figura 7


