| Utiles | Trazados Fund. | Triángulos | Polígonos | Igualdad y Semejanza |
|---|---|---|---|---|
| Potencia. Eje Radical | Homologia y Afinidad | Tangencias | Enlaces, Óvalos, Espirales | Cónicas |
Homología y Afinidad
1.1. Introducción
Se dice que el punto A, es homólogo del punto A’, cuando se cumplen las siguientes condiciones: Fig. 154.
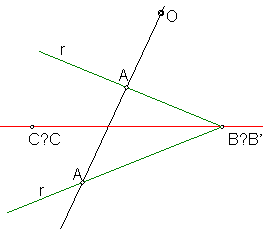
Fig. 154
a) Que estén en línea recta con un punto fijo O, llamado centro de homología.
b) Dos rectas r y r’ son homólogas, cuando se cortan en un mismo punto del eje de homología.
Todos los puntos del eje de homología CC’, son puntos dobles, al ser homólogos de si mismo.
a)Hallar el homólogo del punto 2, conociendo el Centro de homología O, un par de puntos Homólogos 3 y 3’ y el eje de homología e. Fig. 155.
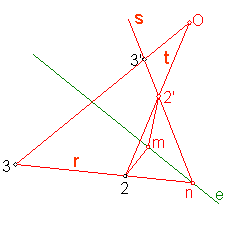
Fig. 155
Unimos los puntos homólogos 3 y 3’, la
recta ha de pasar por O.
Unimos el centro de homología con el punto 2, recta t.
Unimos el punto 3 con el 2, recta s.
Hallamos la recta r, homologa de s, uniendo n con 3’, que corta a t en el punto
Buscado.
Lugar geométrico de los puntos cuyos homólogos del infinito. Serán dos y la representamos por li y li’.
Para hallar las rectas límite procedemos de la forma siguiente:
Partimos de dos rectas homólogas s y s’, del centro de homología O y del eje e. Fig. 156.
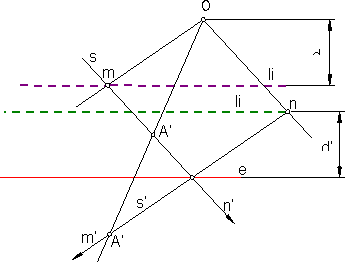
Fig. 156
Trazamos una paralela a la recta s’ por el centro de de homología hasta que corte a la recta s en el punto m.
Por m trazamos la paralela al eje de homología e.
Repetimos la operación para la recta s.
Cuando dos rectas cualquiera se cortan en un mismo punto de la recta límite, sus homólogas son paralelas. Fig. 157.
Sean las rectas s y t, el centro de homología O, la y el eje de homología e.
Trazamos la recta mO.
Las rectas homólogas serán s’ y t’, paralelas a la dirección mO.
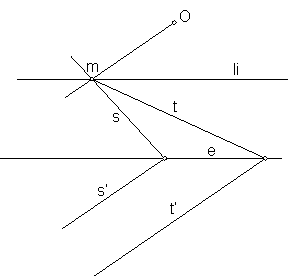
Fig. 157
Dos figuras situadas en un mismo plano son homológicas, cuando se corresponden punto a punto y recta a recta, de tal formas que las rectas que unen pares de puntos homólogos se cortan en un punto dado, centro de homología y los pares de rectas homólogas se cortan en un mismo punto del eje de homología.
a)Dado el eje de homología e, recta límite li, centro de homología o y un polígono A, B, C, D. hallar la figura homóloga. Fig. 158
Prologamos los lados AB y CD, hasta que corten a la recta límite en m y al eje de homología en RS.
Unimos m con O, y por los puntos R y S, trazamos dos paralelas a dicha recta.
Prolongamos los lados AD y CB, hasta que corten a la recta límite en n y al eje en PQ.
Unimos n con O, y por los puntos P y Q, trazamos dos rectas paralelas a dicha dirección.
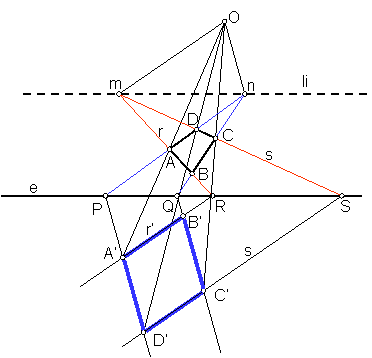
Fig. 158
La figura homóloga quedará determina por los puntos A’, B’, C’, D’.
La afinidad es una transformación geométrica, en el que el centro de afinidad se encuentre en el infinito. Fig. 159.
En toda afinidad debe de cumplirse:
1. Toda recta que une dos puntos afines AA’, son paralelas a la dirección de afinidad.
2. Dos rectas afines r y r’, y se cortan en un mismo punto del eje de afinidad CC’, siendo este un punto doble.
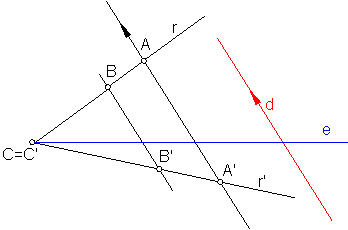
Fig. 159
a) Dado el hexágono a ,b ,c, d, e ,f, el punto homólogo de O y el eje de homología e. Hallar la figura afín. Fig. 160.
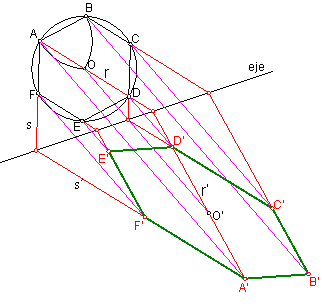
Fig. 160
Unimos O con O’ para hallar la dirección de afinidad d.
Trazamos por los vértices del polígono, paralelas a dicha dirección.
Hallamos la recta r y su afín r’, obteniendo los puntos A’ y D’.
Prolongamos el lado, AF, recta s, hasta que corte al eje e, uniendo este punto con A’.


