| Punto | Recta | Plano | Intersección | Abatimientos y Cambios de Plano | Giros |
| Pirámide | Cono | Cilindro | Prisma | Poliedros |
- 1. GIROS
1.1. GIRO DE UN PUNTO
Los giros son otro de los procedimiento para obtener proyecciones en verdadera magnitud. ( fig 61a y b).

Los resultados son los mismos que con los cambios de planos, pero en este caso los planos de proyección permanecen fijos y son los puntos los que cambian de posición.
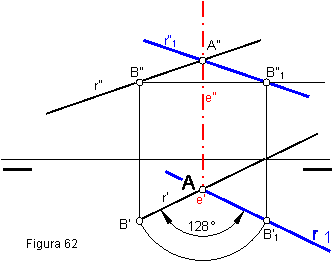
1.2. GIRO DE UNA RECTA OBLICUA A OTRA POSICIÓN DE OBLICUIDAD. ( fig 62)
El giro de una recta, se limita al giro de dos puntos de la misma. Ambos puntos deben girarse en el mismo Sentido y con el mismo ángulo.
El eje de giro puede adoptarse cruzándose con la recta o cortándola. En nuestro caso adoptaremos un eje de giro e’-e”,que corte a la recta r’-r”, y sea perpendicular al plano horizontal.
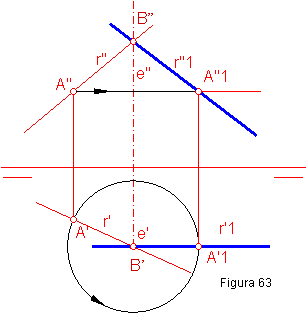
1.3. GIRO DE UNA RECTA OBLICUA A PARALELA AL VERTICAL. ( fig. 63)
Utilizaremos un eje de giro perpendicular al plano horizontal e(e’-e”) y que corte a la recta en el punto B ( B’-B”).
1. Giramos el punto A’, el valor del ángulo preciso para dejarla paralela a la línea de tierra. Ocupando la posición A”1.
2. Por A”, trazamos una recta paralela a la L.T.
3. El punto B ( B’-B”), está abatido en si mismo.