- 1. Paralelismo
1.1. Planos paralelos.

Figura 20
Para que dos planos sean paralelos las l. m. p. tendrán que ser paralelas y estar graduadas en mismo sentido y tener el mismo intervalo. Figura 20.
1.2. Rectas paralelas
Para que dos rectas sean paralelas en el espacio, sus proyecciones sobre el cuadro deberán de cumplir las siguientes condiciones: Figura 21.
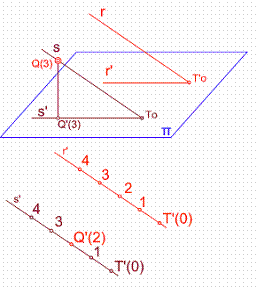
Figura 21-22
a) Sus proyecciones r’ y s’ serán paralelas.
b) Deben de tener el mismo intervalo.
c) Deben estar graduadas en el mismo sentido.
Ejercicio: Trazar por el punto Q (2) una recta s paralela a la dada r. Figura21-22.
Bastará con trazar por el punto Q’ una recta paralela r’ y a continuación graduarla en el mismo sentido y con el mismo intervalo.
1.3. Paralelismo entre recta y plano
Una recta s es paralela a un plano β si lo es una recta cualquiera r contenida en dicho plano. Figura 23.
Ejercicio: Trazar por el punto P’(2) una recta paralela al plano dado por su l.m.p. graduada t’. Figura 23a.
Situamos en el plano una recta cualquiera r’, por el punto P’(2) trazamos una recta s’ paralela a la anterior. Finalizamos graduando la recta s’ con el mismo intervalo y en el mismo sentido.
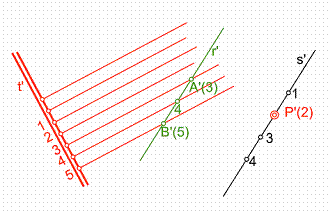
Figura 23
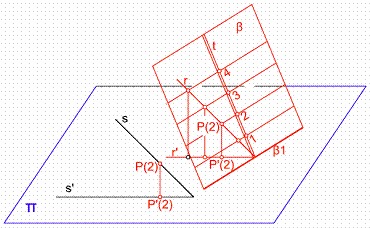
Figura 23a


